CHAPTER – 3
Binary Math and Signed Representations
Representing numbers with bits is one thing. Doing something with
them is an entirely different matter. This chapter discusses some of the
basic mathematical operations that computers perform on binary
numbers along with the binary representations that support those
operations. These concepts will help programmers better understand the
limitations of doing math with a processor, and thereby allow them to
better handle problems such as the upper and lower limits of variable
types, mathematical overflow, and type casting.
3.1 Binary Addition
Regardless of the numbering system, the addition of two numbers
with multiple digits is performed by adding the corresponding digits of
a single column together to produce a single digit result. For example, 3
added to 5 using the decimal numbering system equals 8. The 8 is
placed in the same column of the result where the 3 and 5 came from.
All of these digits, 3, 5, and 8, exist in the decimal numbering system,
and therefore can remain in a single column.
In some cases, the result of the addition in a single column might be
more than 9 making it necessary to place a ‘1’ overflow or carry to the
column immediately to the left. If we add 6 to 5 for example, we get 11
which is too large to fit in a single decimal digit. Therefore, 10 is
subtracted from the result leaving 1 as the new result for that column.
The subtraction of 10 is compensated for by placing a carry in the next
highest column, the ten’s place. Another way of saying this is that 6
added to 5 equals 1 with a carry of 1. It is important to note that the
addition of two digits in decimal can never result in a value greater than
18. Therefore, the carry to the next highest position will never be larger
than 1.
Binary addition works the same way except that we’re limited to two
digits. Three of the addition operations, 0+0, 0+1, and 1+0, result in 0
or 1, digits that already exist in the binary numbering system. This
means no carry will be needed.
43

44 Computer Organization and Design Fundamentals
Adding 1 to 1, however, results in a decimal 2, a digit which does
not exist in binary. In this case, we need to create a carry or overflow
that will go to the next column.
The next highest bit position represents 21 = 2. Just as we did with
decimal, we subtract one instance of the next highest bit position from
our result. In the case of 1+1=2, we subtract 2 from 2 and get 0.
Therefore, 0 is the result that is placed in the current column, and the
subtraction of 2 becomes a carry to the next column. Therefore, 1+1 in
binary equals 0 with a carry of 1. Each of the possible binary additions
of two variables is shown in Figure 3-1.
1
0 0 1 1
+ 0 + 1 + 0 + 1
0 1 1 10
Figure 3-1 Four Possible Results of Adding Two Bits
The last addition 1 + 1 = 10 is equivalent to the decimal addition
2 2 2
1 + 1 = 2 . Converting 2 to binary results in 10 , the result shown
10 10 10 10 2
in the last operation of Figure 3-1, which confirms our work.
Now we need to figure out how to handle a carry from a previous
column. In decimal, a carry from a previous column is simply added to
the next column. This is the same as saying that we are adding three
digits where one of the digits, the carry, is always a one.
In binary, accounting for a carry adds four new scenarios to the
original four shown in Figure 3-1. Just like decimal, it is much like
adding three values together: 1+0+0, 1+0+1, 1+1+0, or 1+1+1. The
four additional cases where a carry is added from the previous column
are shown in Figure 3-2.
Previous 1 1 1
Carry (cid:198) 1 1 1 1
0 0 1 1
+ 0 + 1 + 0 + 1
1 10 10 11
Figure 3-2 Four Possible Results of Adding Two Bits with Carry

Chapter 3: Binary Math and Signed Representations 45
The second and third cases are similar to the last case presented in
Figure 3-1 where two 1’s are added together to get a result of 0 with a
carry. The last case in Figure 3-2, however, has three 1’s added together
which equals 3 . Subtracting 2 from this result places a new result of 1
10
in the current column and sends a carry to the next column. And just as
in decimal addition, the carry in binary is never greater than 1.
Now let’s try to add binary numbers with multiple digits. The
example shown below presents the addition of 10010110 and
2
00101011 . The highlighted values are the carries from the previous
2
column’s addition, and just as in decimal addition, they are added to the
next most significant digit/bit.
1 1 1 1 1
1 0 0 1 0 1 1 0
+ 0 0 1 0 1 0 1 1
1 1 0 0 0 0 0 1
3.2 Binary Subtraction
Just as with addition, we’re going to use the decimal numbering
system to illustrate the process used in the binary numbering system for
subtraction.
There are four possible cases of single-bit binary subtraction: 0 – 0,
0 – 1, 1 – 0, and 1 – 1. As long as the value being subtracted from (the
minuend) is greater than or equal to the value subtracted from it (the
subtrahend), the process is contained in a single column.
Minuend (cid:198) 0 1 1
Subtrahend (cid:198) – 0 – 0 – 1
0 1 0
But what happens in the one case when the minuend is less than the
subtrahend? As in decimal, a borrow must be taken from the next most
significant digit. The same is true for binary.
A “borrow” is made from
the next highest bit position
1 0
– 1
1

46 Computer Organization and Design Fundamentals
Pulling 1 from the next highest column in binary allows us to add 10
2
or a decimal 2 to the current column. For the previous example, 10
2
added to 0 gives us 10 or a decimal 2. When we subtract 1 from 2, the
2
result is 1.
Now let’s see how this works with a multi-bit example.
0 1 0
1 10 10 1 1 1 10 1 1
– 0 0 1 0 1 0 1 0 1
0 1 1 1 0 0 1 1 0
Starting at the rightmost bit, 1 is subtracted from 1 giving us zero. In
the next column, 0 is subtracted from 1 resulting in 1. We’re okay so far
with no borrows required. In the next column, however, 1 is subtracted
from 0. Here we need to borrow from the next highest digit.
The next highest digit is a 1, so we subtract 1 from it and add 10 to
the digit in the 22 column. (This appears as a small “1” placed before
the 0 in the minuend’s 22 position.) This makes our subtraction 10 – 1
which equals 1. Now we go to the 23 column. After the borrow, we
have 0 – 0 which equals 0.
We need to make a borrow again in the third column from the left,
the 26 position, but the 27 position of the minuend is zero and does not
have anything to borrow. Therefore, the next highest digit of the
minuend, the 28 position, is borrowed from. The borrow is then
cascaded down until it reaches the 26 position so that the subtraction
may be performed.
3.3 Binary Complements
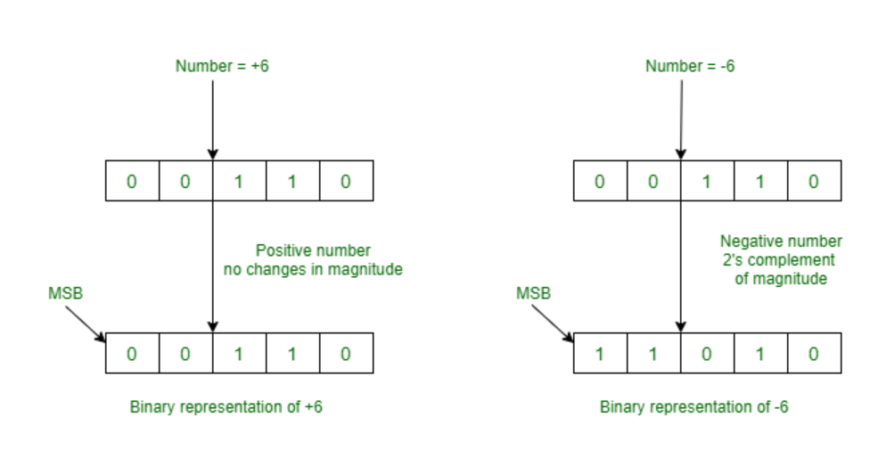
In decimal arithmetic, every number has an additive complement,
i.e., a value that when added to the original number results in a zero.
For example, 5 and -5 are additive complements because 5 + (-5) = 0.
This section describes the two primary methods used to calculate the
complements of a binary value.
3.3.1 One’s Complement
When asked to come up with a pattern of ones and zeros that when
added to a binary value would result in zero, most people respond with,
“just flip each bit in the original value.” This “inverting” of each bit,
substituting 1’s for all of the 0’s and 0’s for all of the 1’s, results in the
1’s complement of the original value. An example is shown below.

Chapter 3: Binary Math and Signed Representations 47
Previous value 1 0 0 1 0 1 1 1
1’s complement 0 1 1 0 1 0 0 0
The 1’s complement of a value is useful for some types of digital
functions, but it doesn’t provide much of a benefit if you are looking for
the additive complement. See what happens when we add a value to its
1’s complement.
1 0 0 1 0 1 1 0
+ 0 1 1 0 1 0 0 1
1 1 1 1 1 1 1 1
If the two values were additive complements, the result should be
zero, right? Well, that takes us to the 2’s complement.
3.3.2 Two’s Complement
The result of adding an n-bit number to its one’s complement is
always an n-bit number with ones in every position. If we add 1 to that
result, our new value is an n-bit number with zeros in every position
and an overflow or carry to the next highest position, the (n+1)th
column which corresponding to 2n. For our 8-bit example above, the
result of adding 10010110 to 01101001 is 11111111 . Adding 1 to
2 2 2
this number gives us 00000000 with an overflow carry of 1 to the
2
ninth or 28 column. If we restrict ourselves to 8 bits, this overflow carry
can be ignored.
This gives us a method for coming up with the additive complement
called the 2’s complement representation. The 2’s complement of a
value is found by first taking the 1’s complement, then incrementing
that result by 1. For example, in the previous section, we determined
that the 1’s complement of 10010111 is 01101000 . If we add 1 to this
2 2
value, we get:
0 1 1 0 1 0 0 0
+ 1
0 1 1 0 1 0 0 1
Therefore, the 2’s complement of 10010111 is 01101001 . Let’s see
2 2
what happens when we try to add the value to its 2’s complement.
| 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 |

48 Computer Organization and Design Fundamentals
1 1 1 1 1 1 1 1
1 0 0 1 0 1 1 1
+ 0 1 1 0 1 0 0 1
0 0 0 0 0 0 0 0
The result is zero! Okay, so most of you caught the fact that I didn’t
drop down the last carry which would’ve made the result 100000000 .
2
This is not a problem, because in the case of signed arithmetic, the
carry has a purpose other than that of adding an additional digit
representing the next power of two. As long as we make sure that the
two numbers being added have the same number of bits, and that we
keep the result to that same number of bits too, then any carry that goes
beyond that should be discarded.
Actually, discarded is not quite the right term. In some cases we will
use the carry as an indication of a possible mathematical error. It should
not, however, be included in the result of the addition. This is simply
the first of many “anomalies” that must be watched when working with
a limited number of bits.
Two more examples of 2’s complements are shown below.
Original value (10 ) 0 0 0 0 1 0 1 0
10
1’s complement 1 1 1 1 0 1 0 1
2’s complement (-10 ) 1 1 1 1 0 1 1 0
10
Original value (88 ) 0 1 0 1 1 0 0 0
10
1’s complement 1 0 1 0 0 1 1 1
2’s complement (-88 ) 1 0 1 0 1 0 0 0
10
Now let’s see if the 2’s complement representation stands up in the
face of addition. If 88 = 01011000 and -10 = 11110110 , then the
10 2 10 2
addition of these two numbers should equal 78 = 01001110 .
10 2
1 1 1 1
0 1 0 1 1 0 0 0
+ 1 1 1 1 0 1 1 0
0 1 0 0 1 1 1 0
| 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |

Chapter 3: Binary Math and Signed Representations 49
There is also a “short-cut” to calculating the 2’s complement of a
binary number. This trick can be used if you find the previous way too
cumbersome or if you’d like a second method in order to verify the
result you got from using the first.
The trick works by copying the zero bit values starting with the least
significant bit until you reach your first binary 1. Copy that 1 too. If the
least significant bit is a one, then only copy that bit. Next, invert all of
the remaining bits. Figure 3-3 presents an example of the short-cut.
First ‘1’ reading
right to left
1 0 1 0 1 0 0 0
0 1 0 1 1 0 0 0
Step 2: Invert Step 1: Copy bits
the remaining up to and including
bits. the first ‘1’.
Figure 3-3 Two’s Complement Short-Cut
This result matches the result for the previous example.
In decimal, the negative of 5 is -5. If we take the negative a second
time, we return to the original value, e.g., the negative of -5 is 5. Is the
same true for taking the 2’s complement of a 2’s complement of a
binary number? Well, let’s see.
The binary value for 45 is 00101101 . Watch what happens when
10 2
we take the 2’s complement twice.
Original value = 45 0 0 1 0 1 1 0 1
1’s complement of 45 1 1 0 1 0 0 1 0
2’s complement of 45 = -45 1 1 0 1 0 0 1 1
1’s complement of -45 0 0 1 0 1 1 0 0
2’s complement of -45 = 45 0 0 1 0 1 1 0 1
It worked! The second time the 2’s complement was taken, the
pattern of ones and zeros returned to their original values. It turns out
that this is true for any binary number of a fixed number of bits.
| 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 |

50 Computer Organization and Design Fundamentals
3.3.3 Most Significant Bit as a Sign Indicator
As was stated earlier, 2’s complement is used to allow the computer
to represent the additive complement of a binary number, i.e., negative
numbers. But there is a problem. As we showed earlier in this section,
taking the 2’s complement of 45 = 00101101 gives us –45 =
10 2 10
11010011 . But in Chapter 2, the eight bit value 11010011 was shown
2 2
to be equal to 27 + 26 + 24 + 21 + 20 = 128 + 64 + 16 + 2 + 1 = 211 . So
10
did we just prove that –45 is equal to 211 ? Or maybe 00101101 is
10 10 2
actually –211 .
10
It turns out that when using 2’s complement binary representation,
half of the binary bit patterns must lose their positive association in
order to represent negative numbers. So is 11010011 –45 or 211 ?
2 10 10
It turns out that 11010011 is one of the bit patterns meant to represent
2
a negative number, so in 2’s complement notation, 11010011 = –45 .
2 10
But how can we tell whether a binary bit pattern represents a positive or
a negative number?
From the earlier description of the 2’s complement short-cut, you
can see that except for two cases, the MSB of the 2’s complement is
always the inverse of the original value. The two cases where this isn’t
true are when all bits of the number except the most significant bit
equal 0 and the most significant bit is a 0 or a 1. In both of these cases,
the 2’s complement equals the original value.
In all other cases, when we apply the shortcut we will always
encounter a 1 before we get to the MSB when reading right to left.
Since every bit after this one will be inverted, then the most significant
bit must be inverted toggling it from its original value. If the original
value has a zero in the MSB, then its 2’s complement must have a one
and vice versa. Because of this characteristic, the MSB of a value can
be used to indicate whether a number is positive or negative and is
called a sign bit.
A binary value with a 0 in the MSB position is considered positive
and a binary value with a 1 in the MSB position is considered negative.
This makes it vital to declare the number of bits that a signed binary
number uses. If this information is not given, then the computer or the
user looking at a binary number will not know which bit is the MSB.
Since the MSB is being used to indicate the sign of a signed binary
number, it cannot be used to represent a power of 2, i.e., if a number is
said to represent a 2’s complement value, only n-1 of its n bits can be

Chapter 3: Binary Math and Signed Representations 51
used to determine the magnitude since the MSB is used for the sign.
This cuts in half the number of positive integers n bits can represent.
And the special cases? Well, a binary number with all zeros is equal
to a decimal 0. Taking the negative of zero still gives us zero. The other
case is a bit trickier. In the section on minimums and maximums, we
will see that an n-bit value with an MSB equal to one and all other bits
equal to zero is a negative number, specifically, –2(n-1). The largest
positive number represented in 2’s complement has an MSB of 0 with
all the remaining bits set to one. This value equals 2(n-1) – 1. Therefore,
since 2(n-1) > 2(n-1) – 1, we can see that there is no positive equivalent to
the binary number 100…00 .
2
3.3.4 Signed Magnitude
A second, less useful way to represent positive and negative binary
numbers is to take the MSB and use it as a sign bit, much like a plus or
minus sign, and leave the remaining bits to represent the magnitude.
The representation is called signed magnitude representation. For
example, –45 and +45 would be identical in binary except for the MSB
which would be set to a 1 for –45 and a 0 for +45. This is shown below
for an 8-bit representation.
+45 in binary 0 0 1 0 1 1 0 1
10
–45 using signed magnitude 1 0 1 0 1 1 0 1
10
3.3.5 MSB and Number of Bits
Since the MSB is necessary to indicate the sign of a binary value, it
is vital that we know how many bits a particular number is being
represented with so we know exactly where the MSB is. In other
words, the leading zeros of a binary value may have been removed
making it look like the binary value is negative since it starts with a
one.
For example, if the binary value 10010100 is assumed to be an 8-bit
2
signed number using 2’s complement representation, then converting it
to decimal would give us -108 . (We will discuss converting signed
10
values to decimal later in this chapter.) If, however, it was a 10-bit
number, then the MSB would be 0 and it would convert to the positive
value 148 .
10
| 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 |

52 Computer Organization and Design Fundamentals
3.3.6 Issues Surrounding the Conversion of Binary Numbers
Since computers don’t use an infinite number of bits to represent
values, the software must know two things before it can interpret a
binary value: the number of bits and the type of binary representation
being used. This usually is confusing for the novice.
Identifying 10100110 as an 8-bit number isn’t enough. Note that the
2
MSB is equal to 1. Therefore, this value represents one number in
unsigned binary, another number in 2’s complement, and yet a third in
signed magnitude.
First, let’s do the conversion of 10100110 assuming it is an 8-bit,
2
unsigned binary like those described in Chapter 2.
10100110 = 27 + 25 + 22 + 21 = 128 + 32 + 4 + 2 = 166
2 10
Now let’s do the conversion in 2’s complement. Before we do,
however, let’s examine the process. First, if the MSB is equal to 0, then
the value is a positive number. In 2’s complement notation, positive
numbers look just like unsigned binary and should be treated exactly
the same when performing a conversion to decimal.
If, however, the MSB is equal to 1, then the value represented by
this pattern of ones and zeros is negative. To turn it into a negative
number, someone had to apply the process of taking the 2’s
complement to the original positive value. Therefore, we must remove
the negative sign before we do the conversion.
It was shown earlier how a second application of the 2’s complement
conversion process returns the number back to its original positive
value. If taking the 2’s complement of a negative number returns it to
its positive value, then the positive value can be converted to decimal
using the same process used for an unsigned binary value. Adding a
negative sign to the decimal result completes the conversion. Figure
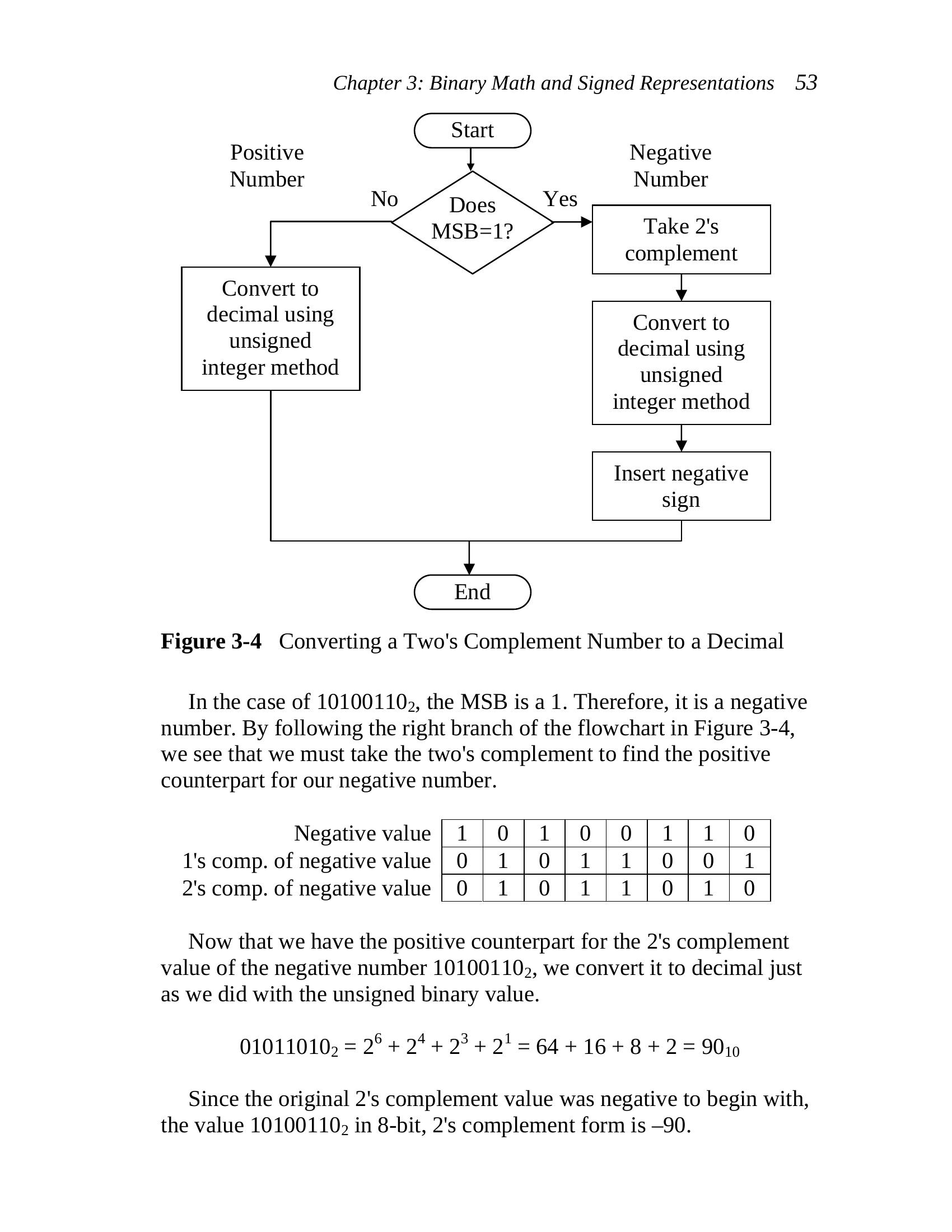
3-4 presents a flow chart showing this process graphically.
A second method of converting an n-bit 2’s complement value to
decimal is to perform the conversion as you would an unsigned binary
value except that the MSB digit is treated as –2n-1 instead of 2n-1. For
example, the MSB of an 8-bit 2’s complement value would represent
–2-7 = –128.

Chapter 3: Binary Math and Signed Representations 53
Start
Positive Negative
Number Number
No Yes
Does
Take 2’s
MSB=1?
complement
Convert to
decimal using
Convert to
unsigned
decimal using
integer method
unsigned
integer method
Insert negative
sign
End
Figure 3-4 Converting a Two’s Complement Number to a Decimal
In the case of 10100110 , the MSB is a 1. Therefore, it is a negative
2
number. By following the right branch of the flowchart in Figure 3-4,
we see that we must take the two’s complement to find the positive
counterpart for our negative number.
Negative value 1 0 1 0 0 1 1 0
1’s comp. of negative value 0 1 0 1 1 0 0 1
2’s comp. of negative value 0 1 0 1 1 0 1 0
Now that we have the positive counterpart for the 2’s complement
value of the negative number 10100110 , we convert it to decimal just
2
as we did with the unsigned binary value.
01011010 = 26 + 24 + 23 + 21 = 64 + 16 + 8 + 2 = 90
2 10
Since the original 2’s complement value was negative to begin with,
the value 10100110 in 8-bit, 2’s complement form is –90.
2
| 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
54 Computer Organization and Design Fundamentals
We can duplicate this result using the second method of conversion,
i.e., converting 10100110 using the unsigned binary method while
2
treating the MSB as –2-7. In this case, there is a 1 in the –2-7, 25, 22, and
21 positions.
10100110 = 2-7 + 25 + 22 + 21 = –128 + 32 + 4 + 2 = –90
2 10
Next, let’s do the conversion assuming 10100110 is in 8-bit signed
2
magnitude where the MSB represents the sign bit. As with the 2’s
complement form, an MSB of 1 means that the number is negative.
The conversion of a signed magnitude binary number to decimal is
different than 2’s complement. In the case of signed magnitude, remove
the MSB and convert the remaining bits using the same methods used
to convert unsigned binary to decimal. When done, place a negative
sign in front of the decimal result only if the MSB equaled 1.
Meaning of bit position Sign 26 25 24 23 22 21 20
Binary value 1 0 1 0 0 1 1 0
To convert this value to a positive number, remove the sign bit.
Next, calculate the magnitude just as we would for the unsigned case.
0100110 = 25 + 22 + 21 = 32 + 4 + 2 = 38
2 10
Since the MSB of the original value equaled 1, the signed magnitude
value was a negative number to begin with, and we need to add a
negative sign. Therefore, 10100110 in 8-bit, signed magnitude
2
representation equals –38 .
10
But what if this binary number was actually a 10-bit number and not
an 8 bit number? Well, if it’s a 10 bit number (0010100110 ), the MSB
2
is 0 and therefore it is a positive number. This makes our conversion
much easier. The method for converting a positive binary value to a
decimal value is the same for all three representations. The conversion
goes something like this:
Bit position MSB 28 27 26 25 24 23 22 21 20
Binary value 0 0 1 0 1 0 0 1 1 0
0010100110 = 27 + 25 + 22 + 21 = 128 + 32 + 4 + 2 = 166
2 10
| Sign | 26 | 25 | 24 | 23 | 22 | 21 | 20 |
| 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
| MSB | 28 | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 |
| 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |

Chapter 3: Binary Math and Signed Representations 55
This discussion shows that it is possible for a binary pattern of ones
and zeros to have three interpretations. It all depends on how the
computer has been told to interpret the value.
In a programming language such as C, the way in which a computer
treats a variable depends on how it is declared. Variables declared as
unsigned int are stored in unsigned binary notation. Variables declared
as int are treated as either 2’s complement or signed magnitude
depending on the processor and/or compiler.
3.3.7 Minimums and Maximums
When using a finite number of bit positions to store information, it is
vital to be able to determine the minimum and maximum values that
each binary representation can handle. Failure to do this might result in
bugs in the software you create. This section calculates the minimum
and maximum values for each of the three representations discussed in
this and the previous chapter using a fixed number of bits, n.
Let’s begin with the most basic representation, unsigned binary. The
smallest value that can be represented with unsigned binary
representation occurs when all the bits equal zero. Conversion from
binary to decimal results in 0 + 0 + … + 0 = 0. Therefore, for an n bit
number:
Minimum n-bit unsigned binary number = 0 (3.1)
The largest value that can be represented with unsigned binary
representation is reached when all n bits equal one. When we convert
this value from binary to decimal, we get 2n-1 + 2n-2 + … + 20. As was
shown in Chapter 2, adding one to this expression results in 2n.
Therefore, for an n-bit unsigned binary number, the maximum is:
Maximum n-bit unsigned binary number = 2n – 1 (3.2)
Next, let’s examine the minimum and maximum values for an n-bit
2’s complement representation. Unlike the unsigned case, the lowest
decimal value that can be represented with n-bits in 2’s complement
representation is not obvious. Remember, 2’s complement uses the
MSB as a sign bit. Since the lowest value will be negative, the MSB
should be set to 1 (a negative value). But what is to be done with all of
the remaining bits? A natural inclination is to set all the bits after the

56 Computer Organization and Design Fundamentals
MSB to one. This should be a really big negative number, right? Well,
converting it to decimal results in something like the 8 bit example
below:
2’s comp. value 1 1 1 1 1 1 1 1
Intermediate 1’s complement 0 0 0 0 0 0 0 0
Positive value of 2’s comp. 0 0 0 0 0 0 0 1
This isn’t quite what we expected. Using the 2’s complement method
to convert 11111111 to a decimal number results in –1 . This couldn’t
2 10
possibly be the lowest value that can be represented with 2’s
complement.
It turns out that the lowest possible 2’s complement value is an MSB
of 1 followed by all zeros as shown in the 8 bit example below. For the
conversion to work, you must strictly follow the sequence presented in
Figure 3-4 to convert a negative 2’s complement value to decimal.
2’s comp. value 1 0 0 0 0 0 0 0
Intermediate 1’s complement 0 1 1 1 1 1 1 1
Positive value of 2’s comp. 1 0 0 0 0 0 0 0
Converting the positive value to decimal using the unsigned method
shows that 10000000 = –27 = –128. Translating this to n-bits gives us:
2
Minimum n-bit 2’s complement number = –2(n-1) (3.3)
The maximum value is a little easier to find. It is a positive number,
i.e., an MSB of 0. The remaining n-1 bits are then treated as unsigned
magnitude representation. Therefore, for n bits:
Maximum n-bit 2’s complement number = 2(n-1) – 1 (3.4)
Last of all, we have the signed magnitude representation. To
determine the magnitude of a signed magnitude value, ignore the MSB
and use the remaining n–1 bits to convert to decimal as if they were in
unsigned representation. This means that the largest and smallest values
represented with an n-bit signed magnitude number equals the positive
and negative values of an (n–1)-bit unsigned binary number.
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |

Chapter 3: Binary Math and Signed Representations 57
Minimum n-bit signed magnitude number = –(2(n-1)– 1) (3.5)
Maximum n-bit signed magnitude number = (2(n-1)– 1) (3.6)
As an example, Table 3-1 compares the minimum and maximum
values of an 8-bit number for each of the binary representations. The
last column shows the number of distinct integer values possible with
each representation. For example, there are 256 integer values between
0 and 255 meaning the 8-bit unsigned binary representation has 256
possible combinations of 1’s and 0’s, each of which represents a
different integer in the range.
Table 3-1 Representation Comparison for 8-bit Binary Numbers
Number of integers
Representation Minimum Maximum
represented
Unsigned 0 255 256
2’s Complement -128 127 256
Signed Magnitude -127 127 255
So why can 8-bit signed magnitude only represent 255 possible
values instead of 256? It is because in signed magnitude 00000000 and
2
10000000 both represent the same number, a decimal 0.
2
3.4 Floating Point Binary
Binary numbers can also have decimal points, and to show you how,
we will once again begin with decimal numbers. For decimal numbers
with decimal points, the standard way to represent the digits to the right
of the decimal point is to continue the powers of ten in descending
order starting with -1 where 10-1=1/10th = 0.1. That means that the
number 6.5342 has 5 increments of 10-1 (tenths), 3 increments of 10-2
(hundredths), 4 increments of 10-3 (thousandths), and 2 increments of
10-4 (ten-thousandths). The table below shows this graphically.
Exponent 3 2 1 0 -1 -2 -3 -4
Position value 1000 100 10 1 0.1 0.01 0.001 0.0001
Sample values 0 0 0 6 5 3 4 2
| Representation | Minimum | Maximum | Number of integers | ||
| None | None | None | None | represented | None |
| Unsigned | 0 | 255 | 256 | None | None |
| 2’s Complement | -128 | 127 | 256 | None | None |
| Signed Magnitude | -127 | 127 | 255 | None | None |
| 3 | 2 | 1 | 0 | -1 | -2 | -3 | -4 |
| 1000 | 100 | 10 | 1 | 0.1 | 0.01 | 0.001 | 0.0001 |
| 0 | 0 | 0 | 6 | 5 | 3 | 4 | 2 |

58 Computer Organization and Design Fundamentals
Therefore, our example has the decimal value 6*1 + 5*0.1 + 3*0.01 +
4*0.001 + 2*0.0001 = 6.5342.
Binary representation of real numbers works the same way except
that each position represents a power of two, not a power of ten. To
convert 10.01101 to decimal for example, use descending negative
powers of two to the right of the decimal point.
Exponent 2 1 0 -1 -2 -3 -4 -5
Position value 4 2 1 0.5 0.25 0.125 0.0625 0.03125
Sample values 0 1 0 0 1 1 0 1
Therefore, our example has the decimal value 0*4 + 1*2 + 0*1
+0*0.5 + 1*0.25 + 1*0.125 + 0*0.0625 + 1*0.03125 = 2.40625. This
means that the method of conversion is the same for real numbers as it
is for integer values; we’ve simply added positions representing
negative powers of two.
Computers, however, use a form of binary more like scientific
notation to represent floating-point or real numbers. For example, with
scientific notation we can represent the large value 342,370,000 as
3.4237 x 108. This representation consists of a decimal component or
mantissa of 3.4237 with an exponent of 8. Both the mantissa and the
exponent are signed values allowing for negative numbers and for
negative exponents respectively.
Binary works the same way using 1’s and 0’s for the digits of the
mantissa and exponent and using 2 as the multiplier that moves the
decimal point left or right. For example, the binary number
100101101.010110 would be represented as:
1.00101101010110 * 28
The decimal point is moved left for negative exponents of two and right
for positive exponents of two.
The IEEE Standard 754 is used to represent real numbers on the
majority of contemporary computer systems. It utilizes a 32-bit pattern
to represent single-precision numbers and a 64-bit pattern to represent
double-precision numbers. Each of these bit patterns is divided into
three parts, each part representing a different component of the real
number being stored. Figure 3-5 shows this partitioning for both single-
and double-precision numbers.
| 2 | 1 | 0 | -1 | -2 | -3 | -4 | -5 |
| 4 | 2 | 1 | 0.5 | 0.25 | 0.125 | 0.0625 | 0.03125 |
| 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 |

Chapter 3: Binary Math and Signed Representations 59
1 bit 8 bits 23 bits
Sign
Exponent, E Fraction, F
bit
a) Single-Precision
1 bit 11 bits 52 bits
Sign
Exponent, E Fraction, F
bit
b) Double-Precision
Figure 3-5 IEEE Standard 754 Floating-Point Formats
Both formats work the same differing only by the number of bits
used to represent each component of the real number. In general, the
components of the single-precision format are substituted into Equation
3.7 where the sign of the value is determined by the sign bit (0 –
positive value, 1 – negative value). Note that E is in unsigned binary
representation.
(+)1.F x 2(E-127) (3.7)
Equation 3.8 is used for the double-precision values.
(+)1.F x 2(E-1023) (3.8)
In both cases, F is preceded with an implied ‘1’ and a binary point.
There are, however, some special cases. These are as follows:
• Positive, E=255, F=0: represents positive infinite;
• Negative, E=255, F=0: represents negative infinite; and
• Positive or negative, E=0, F=0: represents zero.
| Sign bit |
Exponent, E | Fraction, F |
| Sign bit |
Exponent, E | Fraction, F |

60 Computer Organization and Design Fundamentals
Example
Convert the 32-bit single-precision IEEE Standard 754 number
shown below into its binary equivalent.
11010110101101101011000000000000
Solution
First, break the 32-bit number into its components.
1 10101101 01101101011000000000
Sign bit Exponent, E Fraction, F
A sign bit of 1 means that this will be a negative number.
The exponent, E, will be used to determine the power of two by
which our mantissa will be multiplied. To use it, we must first convert
it to a decimal integer using the unsigned method.
Exponent, E = 10101101
2
= 27 + 25 + 23 + 22 + 20
= 128 + 32 + 8 + 4 + 1
= 173
10
Substituting these components into Equation 3.7 gives us:
(+)1.F x 2(E-127) = –1.01101101011000000000000 x 2(173-127)
= –1.01101101011 x 246
Example
Create the 32-bit single-precision IEEE Standard 754 representation
of the binary number 0.000000110110100101
Solution
Begin by putting the binary number above into the binary form of
scientific notation with a single 1 to the left of the decimal point. Note
that this is done by moving the decimal point seven positions to the
right giving us an exponent of –7.

Chapter 3: Binary Math and Signed Representations 61
0.000000110110100101 = 1.10110100101 x 2-7
The number is positive, so the sign bit will be 0. The fraction (value
after the decimal point and not including the leading 1) is 10110100101
with 12 zeros added to the end to make it 23 bits. Lastly, the exponent
must satisfy the equation:
E – 127 = –7
E = –7 + 127 = 120
Converting 120 to binary gives us the 8-bit unsigned binary value
10
01111000 . Substituting all of these components into the IEEE 754
2
format gives us:
0 01111000 10110100101000000000
Sign bit Exponent, E Fraction, F
Therefore, the answer is 00111100010110100101000000000000.
3.5 Hexadecimal Addition
At the beginning of this chapter, it was shown how binary addition
(base 2) with its two digits, 1 and 0, is performed the same way decimal
addition (base 10) is with its ten digits, 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9.
The only difference is the limitation placed on the addition by the
number of digits. In binary, the addition of two or three ones results in
a carry since the result goes beyond 1, the largest binary digit. Decimal
doesn’t require a carry until the result goes beyond 9.
Hexadecimal numbers (base 16) can be added using the same
method. The difference is that there are more digits in hexadecimal
than there are in decimal. For example, in decimal, adding 5 and 7
results in 2 with a carry to the next highest position. In hexadecimal,
however, 5 added to 7 does not go beyond the range of a single digit. In
this case, 5 + 7 = C with no carry. It isn’t until a result greater than F
16 16
is reached (a decimal 15 ) that a carry is necessary.
10
In decimal, if the result of an addition is greater than 9, subtract 10
10
to get the result for the current column and add a carry to the next
column. In binary, when a result is greater than 1, subtract 10 (i.e., 2 )
2 10
to get the result for the current column then add a carry to the next

62 Computer Organization and Design Fundamentals
column. In hexadecimal addition, if the result is greater than F (15 )
16 10
subtract 10 (16 ) to get the result for the current column and add a
16 10
carry to the next column.
D + 5 = 13 + 5 = 18
16 16 10 10 10
By moving a carry to the next highest column, we change the result
for the current column by subtracting 16 .
10
18 = 2 + 16
10 10 10
= 2 with a carry to the next column
16
Therefore, D added to 5 equals 2 with a carry to the next column.
16 16 16
Just like decimal and binary, the addition of two hexadecimal digits
never generates a carry greater than 1. The following shows how
adding the largest hexadecimal digit, F , to itself along with a carry
16
from the previous column still does not require a carry larger than 1 to
the next highest column.
F + F +1 = 15 + 15 + 1 = 31
16 16 10 10 10
= 15 + 16
10 10
= F with a 1 carry to the next column
16
When learning hexadecimal addition, it might help to have a table
showing the hexadecimal and decimal equivalents such as that shown
in Table 3-2. This way, the addition can be done in decimal, the base
with which most people are familiar, and then the result can be
converted back to hex.
Table 3-2 Hexadecimal to Decimal Conversion Table
Hex Dec Hex Dec Hex Dec Hex Dec
0 0 4 4 8 8 C 12
16 10 16 10 16 10 16 10
1 1 5 5 9 9 D 13
16 10 16 10 16 10 16 10
2 2 6 6 A 10 E 14
16 10 16 10 16 10 16 10
3 3 7 7 B 11 F 15
16 10 16 10 16 10 16 10
| Hex | Dec | ||||
| 0 16 |
None | None | 0 10 |
None | None |
| 1 16 |
None | None | 1 10 |
None | None |
| 2 16 |
None | None | 2 10 |
None | None |
| 3 16 |
None | None | 3 10 |
None | None |
| Hex | Dec | ||||
| 4 16 |
None | None | 4 10 |
None | None |
| 5 16 |
None | None | 5 10 |
None | None |
| 6 16 |
None | None | 6 10 |
None | None |
| 7 16 |
None | None | 7 10 |
None | None |
| Hex | Dec | ||||
| 8 16 |
None | None | 8 10 |
None | None |
| 9 16 |
None | None | 9 10 |
None | None |
| A 16 |
None | None | 10 10 |
None | None |
| B 16 |
None | None | 11 10 |
None | None |
| Hex | Dec | ||||
| C 16 |
None | None | 12 10 |
None | None |
| D 16 |
None | None | 13 10 |
None | None |
| E 16 |
None | None | 14 10 |
None | None |
| F 16 |
None | None | 15 10 |
None | None |

Chapter 3: Binary Math and Signed Representations 63
Example
Add 3DA32 to 4292F .
16 16
Solution
Just like in binary and decimal, place one of the numbers to be
added on top of the other so that the columns line up.
3 D A 3 2
+ 4 2 9 2 F
Adding 2 to F goes beyond the limit of digits hexadecimal can
16 16
represent. It is equivalent to 2 + 15 which equals 17 , a value
10 10 10
greater than 16 . Therefore, we need to subtract 10 (16 ) giving us a
10 16 10
result of 1 with a carry into the next position.
1
3 D A 3 2
+ 4 2 9 2 F
1
For the next column, the 161 position, we have 1 + 3 + 2 which
equals 6. This result is less than 16 , so there is no carry to the next
10
column.
1
3 D A 3 2
+ 4 2 9 2 F
6 1
The 162 position has A + 9 which in decimal is equivalent to 10
16 16 10
+ 9 = 19 . Since this is greater than 16 , we must subtract 16 to get
10 10 10 10
the result for the 162 column and add a carry in the 163 column.
1 1
3 D A 3 2
+ 4 2 9 2 F
3 6 1

64 Computer Organization and Design Fundamentals
For the 163 column, we have 1 + D + 2 which is equivalent to
16 16 16
1 + 13 + 2 = 16 . This gives us a zero for the result in the 163
10 10 10 10
column with a carry.
1 1 1
3 D A 3 2
+ 4 2 9 2 F
0 3 6 1
Last of all, 1 + 3 + 4 = 8 which is the same in both decimal and
hexadecimal, so the result is 3DA32 + 4292F = 80361 :
16 16 16
1 1 1
3 D A 3 2
+ 4 2 9 2 F
8 0 3 6 1
3.6 BCD Addition
When we introduced Binary Coded Decimal numbers, we said that
the purpose of these numbers was to provide a quick conversion to
binary that would not be used in mathematical functions. It turns out,
however, that BCD numbers can be added too, there’s just an additional
step that occurs when each column of digits is added.
When two BCD numbers are added, the digits 1010, 1011, 1100,
1101, 1110, and 1111 must be avoided. This is done by adding an
additional step anytime the binary addition of two nibbles results in one
of these illegal values or if a carry is generated. When this happens, the
invalid result is corrected by adding 6 to skip over the illegal values.
For example:
BCD Decimal
0011 3
+1000 +8
1011 Invalid
+0110 +6
10001 11

Chapter 3: Binary Math and Signed Representations 65
This step is also necessary if a carry results from a BCD addition.
BCD Decimal
1001 9
+1000 +8
10001 Carry
+0110 +6
10111 17
3.7 Multiplication and Division by Powers of Two
Due to factors to be examined later in this book, multiplication and
division is a time-intensive operation for processors. Therefore,
programmers and compilers have a trick they use to divide or multiply
binary by powers of two. Examine Table 3-3 to see if you can find a
pattern in the multiples of two of the binary number 1001 .
2
Table 3-3 Multiplying the Binary Value 1001 by Powers of Two
2
Binary
Decimal 28 27 26 25 24 23 22 21 20
9 0 0 0 0 0 1 0 0 1
18 0 0 0 0 1 0 0 1 0
36 0 0 0 1 0 0 1 0 0
72 0 0 1 0 0 1 0 0 0
144 0 1 0 0 1 0 0 0 0
288 1 0 0 1 0 0 0 0 0
Note that multiplying by two has the same effect as shifting all of
the bits one position to the left. Similarly, a division by two is
accomplished by a right shift one position. This is similar to moving a
decimal point right or left when multiplying or dividing a decimal
number by a power of ten.
Since a shift operation is significantly faster than a multiply or
divide operation, compilers will always substitute a shift operation
when a program calls for a multiply or divide by a power of two. For
example, a division by 16 = 24 is equivalent to a right shift by 4 bit
10
positions.
| 9 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 18 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| 36 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| 72 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 144 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 288 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |

66 Computer Organization and Design Fundamentals
This works for all positive binary representations of integers and
real numbers as well as 2’s complement representation of negative
numbers. Care must be taken in a few instances in order to maintain the
data’s integrity.
First, carefully watch the bits that are shifted out to verify that data
isn’t being lost. If during a left shift (multiplication), a one is shifted out
of an unsigned binary value or the MSB of a 2’s complement number
changes, then you’ve gone beyond the range of values for that number
of bits. If during a right shift (division), a one is shifted out of an
integer value, then a decimal value has been truncated.
For negative 2’s complement values, there is an additional concern.
Since the MSB is a sign bit, if we fill in the empty bits coming in from
the left with zeros when performing a right shift, then a negative
number has been turned into a positive number. To avoid this, always
duplicate the sign bit in the MSB for each right shift of a 2’s
complement value.
When shifting 1 0 1 0 0 0 1 0
right, fill in bits to
the left with copies
of the MSB.
1 1 0 1 0 0 0 1
Figure 3-6 Duplicate MSB for Right Shift of 2’s Complement Values
This operation can even be used for some multiplications by
constants other than powers of two. For example, if a processor needed
to multiply a value x by 10, it could first multiply x by 2 (a single left
shift), then multiply x by 8 (a left shift by three bit positions), then add
the two shifted values together. This would still be a time savings over
a multiplication.
A bit shift is easily accomplished in high-level programming
languages such as C. In C, the operator used to perform a left shift is
‘<<‘ while a right shift is ‘>>’. Place the variable to be shifted to the left
of the operator and to the right of the operator, enter the number of
positions to shift. Some sample C code is shown below.
| 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 |

Chapter 3: Binary Math and Signed Representations 67
result = iVal << 3; // Set result equal to iVal
// shifted left 3 places
result = iVal >> 4; // Set result equal to iVal
// shifted right 4 places
The first line of code shifts iVal left three positions before putting
the new value into result. This is equivalent to multiplying iVal by
23 = 8. The second line shifts iVal right 4 positions which has the same
effect as an integer divide by 24 = 16.
3.8 Easy Decimal to Binary Conversion Trick
The fact that a single shift right is equivalent to a division by two
gives us a simple way to convert from decimal integers to unsigned
binary. Each 1 that is shifted out because of a right shift is equivalent to
a remainder of 1 after a division by two. Therefore, if you record the
remainders generated by successive divisions by two, you will find that
you’ve generated the binary equivalent of the original decimal value.
For example, let’s convert the decimal value 156 to binary.
10
156 ÷ 2 = 78 with a remainder of 0
10 10
78 ÷ 2 = 39 with a remainder of 0
10 10
39 ÷ 2 = 19 with a remainder of 1
10 10
19 ÷ 2 = 9 with a remainder of 1
10 10
9 ÷ 2 = 4 with a remainder of 1
10 10
4 ÷ 2 = 2 with a remainder of 0
10 10
2 ÷ 2 = 1 with a remainder of 0
10 10
1 ÷ 2 = 0 with a remainder of 1
10 10
Listing the remainders by reversing the order in which they were
generated gives us 10011100 , the binary value for 156 .
2 10
3.9 Arithmetic Overflow
In Section 3.3, the carry was ignored when two 2’s complement
values were added. This is not always the case. For some numbering
systems, a carry is an indication that an error has occurred.
An arithmetic overflow error occurs when two numbers are added
and the result falls outside the valid range of the binary representation
being used. For example, the numbers 200 and 175 can be
10 10
represented in 8-bit unsigned binary notation. The result of their

68 Computer Organization and Design Fundamentals
addition, however, 375 , is not. Therefore, the following 8-bit binary
10
addition (200 + 175 ) results in an error.
10 10
1
1 1 0 0 1 0 0 0
+ 1 0 1 0 1 1 1 1
0 1 1 1 0 1 1 1
Remember that the result must have the same bit count as the
sources, and in this case, the 8-bit unsigned binary result 01110111
2
equals 119 , not 375 .
10 10
When adding unsigned binary values, there is a simple way to
determine if an arithmetic overflow has occurred. In unsigned binary
addition, if a carry is produced from the column representing the MSBs
thereby requiring another bit for the representation, an overflow has
occurred.
In 2’s complement addition, there is a different method for
determining when an arithmetic overflow has occurred. To begin with,
remember that an arithmetic overflow occurs when the result falls
outside the minimum and maximum values of the representation. In the
case of 2’s complement representation, those limits are defined by
Equations 3.3 and 3.4.
The only way that this can happen is if two numbers with the same
sign are added together. It is impossible for the addition of two numbers
with different signs to result in a value outside of the range of 2’s
complement representation.
When two numbers of the same sign are added together, however,
there is a simple way to determine if an error has occurred. If the result
of the addition has the opposite sign of the two numbers being added,
then the result is in error. In other words, if the addition of two positive
numbers resulted in a negative number, or if the addition of two
negative numbers resulted in a positive number, there were not enough
bits in the representation to hold the result. The example below presents
one possible case.
2’s complement Decimal
01100011 99
+00110101 +53
10011000 -104

Chapter 3: Binary Math and Signed Representations 69
If this had been done assuming unsigned notation, the result of 152
10
would have been fine because no carry was generated. From equation
3.4, however, we see that the largest value that 8-bit 2’s complement
representation can hold is 2(8-1) – 1 = 127 . Since 152 is greater than
10 10
127 , it is outside the range of 8-bit 2’s complement representation. In
10
2’s complement representation, the bit pattern 10011000 actually
2
represents -104 .
10
3.10 What’s Next?
Computers use different numeric representations depending on the
application. For example, a person’s weight may be stored as a 16-bit
integer while their house address may be stored in BCD. At this point,
five binary representations have been introduced (unsigned binary,
signed magnitude, 2’s complement, BCD, and floating-point), and
hexadecimal representation has been presented as a quick means for
writing binary values.
Computers, however, do more with numbers than simply represent
them. In Chapter 4, logic gates, the components that computers use to
manipulate binary signals, will be presented. They are the lowest-level
of computer hardware that we will be examining. We will use them to
begin constructing the more complex components of the computer.
Problems
1. True or False: 01101011 has the same value in both unsigned and
2
2’s complement form.
2. True or False: The single-precision floating-point number
10011011011010011011001011000010 is negative.
3. What is the lowest possible value for an 8-bit signed magnitude
binary number?
4. What is the highest possible value for a 10-bit 2’s complement
binary number?
5. Convert each of the following decimal values to 8-bit 2’s
complement binary.
a) 54 b) –49 c) –128 d) –66 e) –98
10 10 10 10 10
6. Convert each of the following 8-bit 2’s complement binary
numbers to decimal.
a) 10011101 b) 00010101 c) 11100110 d) 01101001
2 2 2 2

70 Computer Organization and Design Fundamentals
7. Convert each of the following decimal values to 8-bit signed
magnitude binary.
a) 54 b) –49 c) –127 d) –66 e) –98
10 10 10 10 10
8. Convert each of the following 8-bit signed magnitude binary
numbers to decimal.
a) 10011101 b) 00010101 c) 11100110 d) 01101001
2 2 2 2
9. Convert 1101.0011011 to decimal.
2
10. Convert 10101.11101 to decimal.
2
11. Convert 1.00011011101 x 234 to IEEE Standard 754 for single-
precision floating-point values.
12. Convert the IEEE Standard 754 number
11000010100011010100000000000000 to its binary equivalent.
13. Using hexadecimal arithmetic, add 4D231 to A413F .
16 16
14. Using BCD arithmetic, add 0111010010010110 to
1000001001100001.
15. Why is the method of shifting bits left or right to produce
multiplication or division results by a power of 2 preferred?
16. How many positions must the number 0001101101 be shifted left
2
in order to multiply it by 8?
17. True or False: Adding 01101101 to 10100010 in 8-bit unsigned
2 2
binary will cause an overflow.
18. True or False: Adding 01101101 to 10100010 in 8-bit 2’s
2 2
complement binary will cause an overflow.
19. What would be the best binary representation for each of the
following applications?
– Phone number
– Age (positive integer)
– Exam grade
– Checking account balance
– Value read from a postal scale
– Price