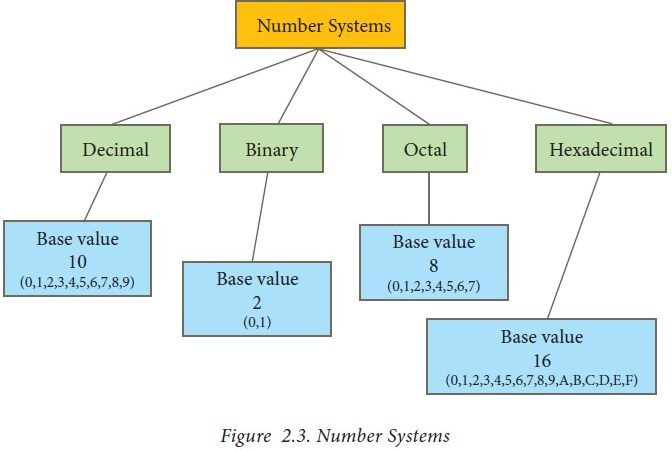
CHAPTER – 2
Numbering Systems
Chapter one discussed how computers remember numbers using
transistors, tiny devices that act like switches with only two positions,
on or off. A single transistor, therefore, can only remember one of two
possible numbers, a one or a zero. This isn’t useful for anything more
complex than controlling a light bulb, so for larger values, transistors
are grouped together so that their combination of ones and zeros can be
used to represent larger numbers.
This chapter discusses some of the methods that are used to
represent numbers with groups of transistors or bits. The reader will
also be given methods for calculating the minimum and maximum
values of each representation based on the number of bits in the group.
2.1 Unsigned Binary Counting
The simplest form of numeric representation with bits is unsigned
binary. When we count upward through the positive integers using
decimal, we start with a 0 in the one’s place and increment that value
until we reach the upper limit of a single digit, i.e., 9. At that point,
we’ve run out of the “symbols” we use to count, and we need to
increment the next digit, the ten’s place. We then reset the one’s place to
zero, and start the cycle again.
Ten’s One’s
place place
0
1
2
3
:
8
9
1 0
Figure 2-1 Counting in Decimal
Since computers do not have an infinite number of transistors, the
number of digits that can be used to represent a number is limited. This
17

18 Computer Organization and Design Fundamentals
would be like saying we could only use the hundreds, tens, and ones
place when counting in decimal.
This has two results. First, it limits the number of values we can
represent. For our example where we are only allowed to count up to
the hundreds place in decimal, we would be limited to the range of
values from 0 to 999.
Second, we need a way to show others that we are limiting the
number of digits. This is usually done by adding leading zeros to the
number to fill up any unused places. For example, a decimal 18 would
be written 018 if we were limited to three decimal digits.
Counting with bits, hereafter referred to as counting in binary, is
subject to these same issues. The only difference is that decimal uses
ten symbols (0, 1, 2, 3, 4, 5, 6, 7, 8, and 9) while binary only uses two
symbols (0 and 1).
To begin with, Figure 2-2 shows that when counting in binary, we
run out of symbols quickly requiring the addition of another “place”
after only the second increment.
Another digit is added when we run
0
out of symbols for the first column.
1
10
11
Another digit is added when we run out
100
of symbols for the second column.
101
Figure 2-2 Counting in Binary
If we were counting using four bits, then the sequence would look
like: 0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000, 1001,
1010, 1011, 1100, 1101, 1110, and 1111. Notice that when restricted to
four bits, we reach our limit at 1111, which happens to be the fifteenth
value. It should also be noted that we ended up with 2 x 2 x 2 x 2 = 16
different values. With two symbols for each bit, we have 2n possible
combinations of symbols where n represents the number of bits.
In decimal, we know what each digit represents: ones, tens,
hundreds, thousands, etc. How do we figure out what the different
digits in binary represent? If we go back to decimal, we see that each
place can contain one of ten digits. After the ones digit counts from 0 to

Chapter 2: Numbering Systems 19
9, we need to increment the tens place. Subsequently, the third place is
incremented after 9 tens and 9 ones, i.e., 99 increments, have been
counted. This makes it the hundreds place.
In binary, the rightmost place is considered the ones place just like
decimal. The next place is incremented after the ones place reaches 1.
This means that the second place in binary represents the value after 1,
i.e., a decimal 2. The third place is incremented after a 1 is in both the
ones place and the twos place, i.e., we’ve counted to a decimal 3.
Therefore, the third place represents a decimal 4. Continuing this
process shows us that each place in binary represents a successive
power of two.
Figure 2-3 uses 5 bits to count up to a decimal 17. Examine each
row where a single one is present in the binary number. This reveals
what that position represents. For example, a binary 01000 is shown to
be equivalent to a decimal 8. Therefore, the fourth bit position from the
right is the 8’s position.
Decimal Binary Decimal Binary
value value value value
0 00000 9 01001
1 00001 10 01010
2 00010 11 01011
3 00011 12 01100
4 00100 13 01101
5 00101 14 01110
6 00110 15 01111
7 00111 16 10000
8 01000 17 10001
Figure 2-3 Binary-Decimal Equivalents from 0 to 17
This information will help us develop a method for converting
unsigned binary numbers to decimal and back to unsigned binary.
Some of you may recognize this as “base-2” math. This gives us a
method for indicating which representation is being used when writing
a number down on paper. For example, does the number 100 represent
a decimal value or a binary value? Since binary is base-2 and decimal
is base-10, a subscript “2” is placed at the end of all binary numbers in
| Decimal | Binary | ||||
| None | value | None | None | value | None |
| 0 | None | None | 00000 | None | None |
| 1 | None | None | 00001 | None | None |
| 2 | None | None | 00010 | None | None |
| 3 | None | None | 00011 | None | None |
| 4 | None | None | 00100 | None | None |
| 5 | None | None | 00101 | None | None |
| 6 | None | None | 00110 | None | None |
| 7 | None | None | 00111 | None | None |
| 8 | None | None | 01000 | None | None |
| Decimal | Binary | ||||
| None | value | None | None | value | None |
| 9 | None | None | 01001 | None | None |
| 10 | None | None | 01010 | None | None |
| 11 | None | None | 01011 | None | None |
| 12 | None | None | 01100 | None | None |
| 13 | None | None | 01101 | None | None |
| 14 | None | None | 01110 | None | None |
| 15 | None | None | 01111 | None | None |
| 16 | None | None | 10000 | None | None |
| 17 | None | None | 10001 | None | None |

20 Computer Organization and Design Fundamentals
this book and a subscript “10” is placed at the end of all decimal
numbers. This means a binary 100 should be written as 100 and a
2
decimal 100 should be written as 100 .
10
2.2 Binary Terminology
When writing values in decimal, it is common to separate the places
or positions of large numbers in groups of three digits separated by
commas. For example, 345323745 is typically written 345,323,745
10 10
showing that there are 345 millions, 323 thousands, and 745 ones. This
practice makes it easier to read and comprehend the magnitude of the
numbers. Binary numbers are also divided into components depending
on their application. Each binary grouping has been given a name.
To begin with, a single place or position in a binary number is called
a bit, short for binary digit. For example, the binary number 0110 is
2
made up of four bits. The rightmost bit, the one that represents the ones
place, is called the Least Significant Bit or LSB. The leftmost bit, the
one that represents the highest power of two for that number, is called
the Most Significant Bit or MSB. Note that the MSB represents a bit
position. It doesn’t mean that a ‘1’ must exist in that position.
The next four terms describe how bits might be grouped together.
• Nibble – A four bit binary number
• Byte – A unit of storage for a single character, typically an eight
bit (2 nibble) binary number (short for binary term)
• Word – Typically a sixteen bit (2 byte) binary number
• Double Word – A thirty-two bit (2 word) binary number
The following are some examples of each type of binary number.
Bit 1
2
Nibble 1010
2
Byte 10100101
2
Word 1010010111110000
2
Double Word 10100101111100001100111011101101
2
2.3 Unsigned Binary to Decimal Conversion
As shown in section 2.1, each place or position in a binary number
corresponds to a specific power of 2 starting with the rightmost bit

Chapter 2: Numbering Systems 21
which represents 20=1. It is through this organization of the bits that we
will convert binary numbers to their decimal equivalent. Figure 2-4
shows the bit positions and the corresponding powers of two for each
bit in positions 0 through 7.
Numbered bit
7 6 5 4 3 2 1 0
position
Corresponding
27 26 25 24 23 22 21 20
power of 2
Decimal equivalent
128 64 32 16 8 4 2 1
of power of 2
Figure 2-4 Values Represented By Each of the First 8 Bit Positions
To begin converting an unsigned binary number to decimal, identify
each bit position that contains a 1. It is important to note that we
number the bit positions starting with 0 identifying the rightmost bit.
Next, add the powers of 2 for each position containing a 1. This sum
is the decimal equivalent of the binary value. An example of this
process is shown in Figure 2-5 where the binary number 10110100 is
2
converted to its decimal equivalent.
Bit Position 7 6 5 4 3 2 1 0
Binary Value 1 0 1 1 0 1 0 0
10110100 = 27 + 25 + 24 + 22
2
= 128 + 32 + 16 + 4
10 10 10 10
= 180
10
Figure 2-5 Sample Conversion of 10110100 to Decimal
2
This brings up an important issue when representing numbers with a
computer. Note that when a computer stores a number, it uses a limited
number of transistors. If, for example, we are limited to eight
transistors, each transistor storing a single bit, then we have an upper
limit to the size of the decimal value we can store.
| Numbered bit position |
7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| Corresponding power of 2 |
27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 |
| Decimal equivalent of power of 2 |
128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | ||||||||
| 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |

22 Computer Organization and Design Fundamentals
The largest unsigned eight bit number we can store has a 1 in all
eight positions, i.e., 11111111 . This number cannot be incremented
2
without forcing an overflow to the next highest bit. Therefore, the
largest decimal value that 8 bits can represent in unsigned binary is the
sum of all powers of two from 0 to 7.
11111111 = 27 + 26 + 25 + 24 + 23 + 22 + 21 + 20
2
= 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1
= 255
10
If you add one to this value, the result is 256 which is 28, the power
of two for the next bit position. This makes sense because if you add 1
to 11111111 , then beginning with the first column, 1 is added to 1
2
giving us a result of 0 with a 1 carry to the next column. This
propagates to the MSB where a final carry is passed to the ninth bit.
The final value is then 100000000 = 256 .
2 10
11111111 + 1 = 100000000 = 256 = 28
2 2 10
Therefore, the maximum value that can be represented with 8 bits in
unsigned binary is 28 – 1 = 255.
It turns out that the same result is found for any number of bits. The
maximum value that can be represented with n bits in unsigned binary
is 2n – 1.
Max unsigned binary value represented with n bits = 2n – 1 (2.1)
We can look at this another way. Each digit of a binary number can
take on 2 possible values, 0 and 1. Since there are two possible values
for the first digit, two possible values for the second digit, two for the
third, and so on until you reach the n-th bit, then we can find the total
number of possible combinations of 1’s and 0’s for n-bits by
multiplying 2 n-times, i.e., 2n.
How does this fit with our upper limit of 2n-1? Where does the “-1”
come from? Remember that counting using unsigned binary integers
begins at 0, not 1. Giving 0 one of the bit patterns takes one away from
the maximum value.

Chapter 2: Numbering Systems 23
2.4 Decimal to Unsigned Binary Conversion
Converting from decimal to unsigned binary is a little more
complicated, but it still isn’t too difficult. Once again, there is a well-
defined process.
To begin with, it is helpful to remember the powers of 2 that
correspond to each bit position in the binary numbering system. These
were presented in Figure 2-4 for the powers of 20 up to 27.
What we need to do is separate the decimal value into its power of 2
components. The easiest way to begin is to find the largest power of 2
that is less than or equal to our decimal value. For example if we were
converting 75 to binary, the largest power of 2 less than or equal to
10
75 is 26 = 64.
10
The next step is to place a 1 in the location corresponding to that
power of 2 to indicate that this power of 2 is a component of our
original decimal value.
Next, subtract this first power of 2 from the original decimal value.
In our example, that would give us 75 – 64 = 11 . If the result is not
10 10 10
equal to zero, go back to the first step where we found the largest
power of 2 less than or equal to the new decimal value. In the case of
our example, we would be looking for the largest power of 2 less than
or equal to 11 which would be 23 = 8.
10
When the result of the subtraction reaches zero, and it eventually
will, then the conversion is complete. Simply place 0’s in the bit
positions that do not contain 1’s. Figure 2-6 illustrates this process
using a flowchart.
If you get all of the way to bit position zero and still have a non-zero
result, then one of two things has happened. Either there was an error in
one of your subtractions or you did not start off with a large enough
number of bits. Remember that a fixed number of bits, n, can only
represent an integer value up to 2n – 1. For example, if you are trying to
convert 312 to unsigned binary, eight bits will not be enough because
10
the highest value eight bits can represent is 28 – 1 = 255 . Nine bits,
10
however, will work because its maximum unsigned value is 29 – 1 =
511 .
10

24 Computer Organization and Design Fundamentals
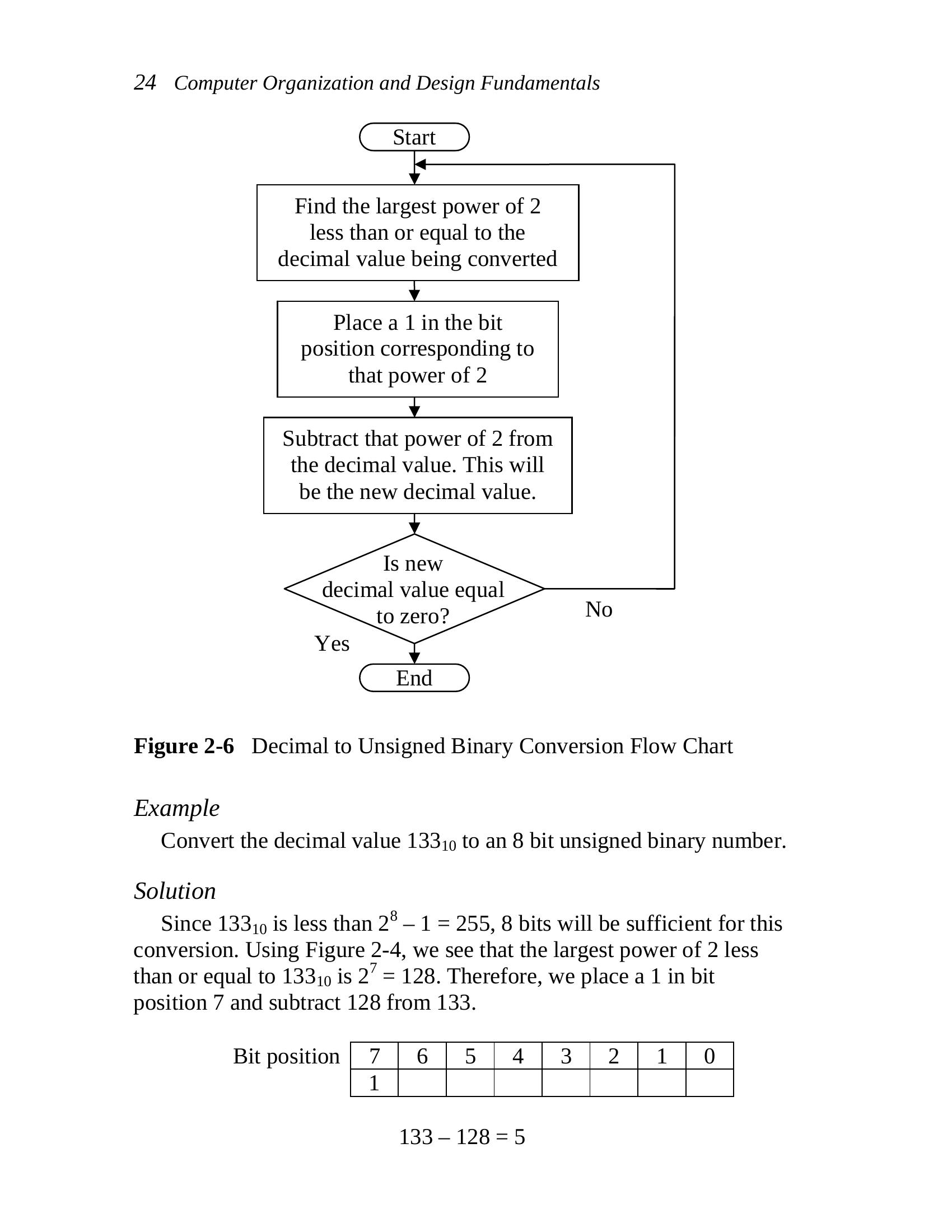
Start
Find the largest power of 2
less than or equal to the
decimal value being converted
Place a 1 in the bit
position corresponding to
that power of 2
Subtract that power of 2 from
the decimal value. This will
be the new decimal value.
Is new
decimal value equal
No
to zero?
Yes
End
Figure 2-6 Decimal to Unsigned Binary Conversion Flow Chart
Example
Convert the decimal value 133 to an 8 bit unsigned binary number.
10
Solution
Since 133 is less than 28 – 1 = 255, 8 bits will be sufficient for this
10
conversion. Using Figure 2-4, we see that the largest power of 2 less
than or equal to 133 is 27 = 128. Therefore, we place a 1 in bit
10
position 7 and subtract 128 from 133.
Bit position 7 6 5 4 3 2 1 0
1
133 – 128 = 5
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 |
Chapter 2: Numbering Systems 25
Our new decimal value is 5. Since this is a non-zero value, our next
step is to find the largest power of 2 less than or equal to 5. That would
be 22 = 4. So we place a 1 in the bit position 2 and subtract 4 from 5.
Bit position 7 6 5 4 3 2 1 0
1 1
5 – 4 = 1
Our new decimal value is 1, so find the largest power of 2 less than
or equal to 1. That would be 20 = 1. So we place a 1 in the bit position 0
and subtract 1 from 1.
Bit position 7 6 5 4 3 2 1 0
1 1 1
1 – 1 = 0
Since the result of our last subtraction is 0, the conversion is
complete. Place zeros in the empty bit positions.
Bit position 7 6 5 4 3 2 1 0
1 0 0 0 0 1 0 1
And the result is:
133 = 10000101
10 2
2.5 Binary Representation of Analog Values
Converting unsigned (positive) integers to binary is only one of the
many ways that computers represent values using binary bits. This
chapter still has two more to cover, and Chapter 3 will cover even
more.
This section focuses on the problems and solutions of trying to map
real world values such as temperature or weight from a specified range
to a binary integer. For example, a computer that uses 8 bits to
represent an integer is capable of representing 256 individual values
from 0 to 255. Temperature, however, is a floating-point value with
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 |
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 |
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |

26 Computer Organization and Design Fundamentals
unrealistic upper and lower limits. Can we get a computer to represent a
temperature using eight bits? The answer is yes, but it will cost us in
the areas of resolution and range.
Another example of analog values is the pattern of sound waves
such as that from music. Figure 2-7 represents such a signal.
Figure 2-7 Sample Analog Signal of Sound
Remember that a single binary bit can be set to only one of two
values: logic 1 or logic 0. Combining many bits together allows for a
range of integers, but these are still discrete values. The real world is
analog, values represented with floating-point measurements capable of
infinite resolution. To use an n-bit binary number to represent analog,
we need to put some restrictions on what is being measured.
First, an n-bit binary number has a limited range. We saw this when
converting unsigned positive integers to binary. In this case, the lower
limit was 0 and the upper limit was 2n-1. To use n-bits to represent an
analog value, we need to restrict the allowable range of analog
measurements. This doesn’t need to be a problem.
For example, does the typical bathroom scale need to measure
values above 400 pounds? If not, then a digital system could use a 10-
bit binary number mapped to a range from zero to 400 pounds. A
binary 0000000000 could represent zero pounds while 1111111111
2 2
could represent 400 pounds.
What is needed next is a method to map the values inside the range
zero to 400 pounds to the binary integers in the range 0000000000 to
2
1111111111 . To do this, we need a linear function defining a one-to-
2
one mapping between each binary integer and the analog value it
represents. To do this, we turn to the basic math expression for a linear
function.
y = mx + b

Chapter 2: Numbering Systems 27
This function defines m as the rate of the change in y with respect to
changes in x and b as the value y is set to when x equals 0. We can use
this expression to map a binary integer x to an analog value y.
The slope of this function, m, can be calculated by dividing the
range of analog values by the number of intervals defined by the n-bit
binary integer. The number of intervals defined by the n-bit binary
integer is equal to the upper limit of that binary number if it were being
used as an unsigned integer, i.e., 2n-1.
Range of analog values
m =
Number of intervals of binary integer
Max analog value – Min analog value
m = (2.2)
2n – 1
Let’s go back to our example of the kitchen scale where the
maximum analog value is 400 pounds while the minimum is zero
pounds. If a 10-bit binary value is used to represent this analog value,
then the number of intervals of the binary integer is 210 – 1 = 1023.
This gives us a slope of:
400 pounds – 0 pounds
m = = 0.391 pounds/binary increment
1023 binary increments
That means that each time the binary number increments, e.g.,
0110110010 goes to 0110110011 , it represents an increment in the
2 2
analog value of 0.391 pounds. Since a binary value of 0000000000
2
represents an analog value of 0 pounds, then 0000000001 represents
2
0.391 pounds, 0000000010 represents 2 × 0.391 = 0.782 pounds,
2
0000000011 represents 3 × 0.391 = 1.173 pounds, and so on.
2
In some cases, the lower limit might be something other than 0. This
is important especially if better accuracy is required. For example, a
kitchen oven may have an upper limit of 600oF. If zero were used as the
lower limit, then the temperature range 600oF – 0oF = 600oF would
need to be mapped to the 2n possible binary values of an n-bit binary
number. For a 9-bit binary number, this would result in an m of:
600oF– 0oF
m = = 1.1742 degrees/binary increment
29 – 1

28 Computer Organization and Design Fundamentals
Does an oven really need to measure values below 100oF though? If
not, a lower limit of 100oF could be used reducing the size of the
analog range to 500oF. This smaller range would improve the accuracy
of the system because each change in the binary value would result in a
smaller increment in the analog value.
600oF– 100oF
m = = 0.9785 degrees/binary increment
29 – 1
The smaller increment means that each binary value will be a more
accurate representation of the analog value.
This non-zero lower limit is realized as a non-zero value for b in the
linear expression y=mx + b. Since y is equal to b when x is equal to
zero, then b must equal the lower limit of the range.
b = Minimum analog value 2.3
The final expression representing the conversion between an analog
value at its binary representation is shown in Equation 2.4.
A – A
( max min )
(2.4)
A calc = 2n – 1 * X + A min
where:
A = analog value represented by binary value
calc
A = maximum analog value
max
A = minimum analog value
min
X = binary value representing analog value
n = number of bits in binary value
Example
Assume that the processor monitoring the temperature of an oven
with a temperature range from 100oF to 600oF measures a 9-bit binary
value of 011001010 . What temperature does this represent?
2
Solution
Earlier, we calculated the rate of change, m, for an oven with a
temperature range from 100oF to 600oF is 500oF ÷ 511 binary

Chapter 2: Numbering Systems 29
increments. Substituting this along with our minimum analog value of
100oF into Equation 2.4 gives us:
500
temperature = oF/binary increment * binary value + 100oF
511
If the processor monitoring the temperature of this oven reads a
binary value of 011001010 , the approximate temperature can be
2
determined by converting 011001010 to decimal and inserting it into
2
the equation above.
011001010 = 27 + 26 + 23 + 21
2
= 128 + 64 + 8 + 2
= 202
10
500oF
temperature = * 202 + 100oF
511
temperature = 297.65oF
The value from the above example is slightly inaccurate. The binary
value 011001010 actually represents a range of values 0.9785oF wide
2
centered around or with a lower limit of 297.65oF. Only a binary value
with an infinite number of bits would be entirely accurate. Since this is
not possible, there will always be a gap or resolution associated with a
digital system due to the quantized nature of binary integer values. That
gap is equivalent to the increment or rate of change of the linear
expression.
Analog range
Resolution = (2.5)
2n – 1
Example
Assume that the analog range of a system using a 10-bit analog-to-
digital converter goes from a lower limit of 5 ounces to an upper limit
of 11 ounces. What is the resolution of this system?
Solution
To determine the resolution, we begin with the analog range.

30 Computer Organization and Design Fundamentals
Analog range = Max analog value – Min analog value
= 11 ounces – 5 ounces
= 6 ounces
Substituting this range into equation 2.5 and using n=10 to represent
the number of bits, we get:
6 ounces
Resolution =
210 – 1
6 ounces
=
1023 increments
= 0.005865 oz/inc
If we examine the results of the example above, we see that our
system can measure 0 ounces, 0.005865 ounces, 0.011730 ounces, (2 *
0.005865 ounces), 0.017595 (3 * 0.005865 ounces), and so on, but it
can never represent the measurement 0.015 ounces. Its resolution is not
that good. In order to get that resolution, you would need to increase
the number of bits in the binary integer or reduce the analog range.
Example
How many bits would be needed for the example above to improve
the resolution to better than 0.001 ounces per increment?
Solution
Each time we increase the number of bits in our binary integer by
one, the number of increments in the range is approximately doubled.
For example, going from 10 bits to 11 bits increases the number of
increments in the range from 210 – 1 = 1023 to 211 – 1 = 2047. The
question is how high do we have to go to get to a specified resolution?
To answer that, let’s begin by setting Equation 2.5 to represent the fact
that we want a resolution of better than 0.001 ounces/increment.
6 ounces
0.001 oz/inc. >
2n – 1
Solving for 2n – 1 gives us:

Chapter 2: Numbering Systems 31
6 ounces
2n – 1 >
0.001 oz/inc.
2n – 1 > 6,000 increments
By substituting different integers for n into the above equation, we
find that n=13 is the lowest value of n for which a resolution better than
0.001 ounces/increment is reached. n=13 results in a resolution of
6 ÷ 8191 = 0.0007325 ounces/increment.
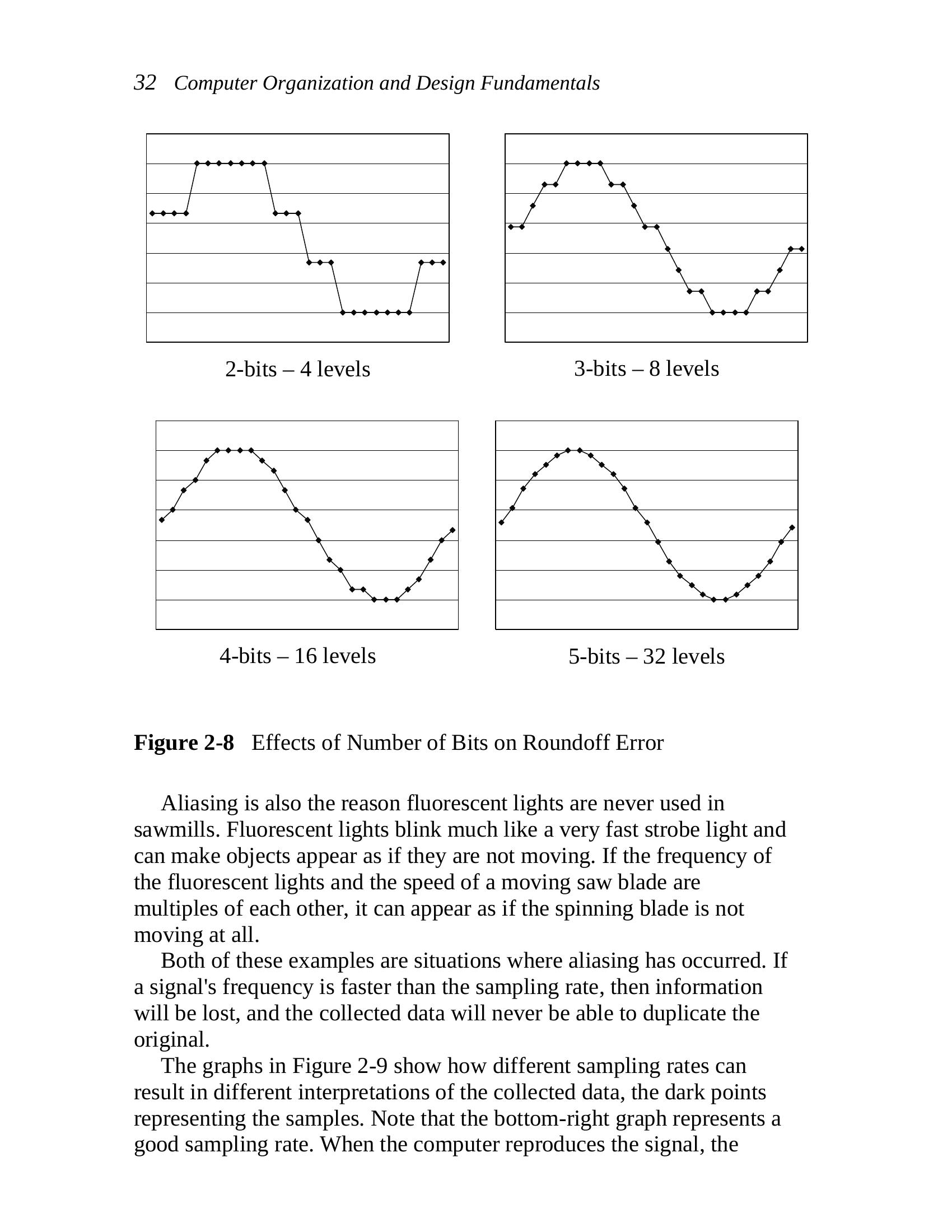
2.6 Sampling Theory
The previous discussion of the integer representation of analog
values shows how the number of bits can affect the roundoff error of
the representation. In general, an n-bit analog-to-digital converter
divides the analog range into 2n – 1 increments. Figure 2-8 presents
four graphs, each with a different number of bits providing different
levels of resolution. The figure shows how the addition of a bit can
improve the resolution of the values represented by the binary integers.
Earlier, it was mentioned how a computer can only capture a “snap
shot” or sample of an analog voltage. This is sufficient for slowly
varying analog values, but if a signal is varying quickly, details might
be missed. To improve the signal’s digital representation, the rate at
which the samples are taken, the sampling rate, needs to be increased.
There is also a chance of missing a higher frequency because the
sampling rate is too slow. This is called aliasing, and there are
examples of it in everyday life.
When riding in a car at night, you may have noticed that at times the
wheels of an adjacent car appear to be spinning at a different rate than
they really are or even appear to spin backwards. (If you have no idea
what I’m talking about, watch the wheels of the car next to you the next
time you are a passenger riding at night under street lights.)
The effect is caused by the fact that the light from street lamps
actually pulses, a fact that is usually not detectable with the human eye.
This pulsing provides a sampling rate, and if the sampling rate is not
fast enough for the spinning wheel, the wheel appears to be spinning at
a different rate than it really is. Street lights are not necessary to see this
effect. Your eye has a sampling rate of its own which means that you
may experience this phenomenon in the day time.

32 Computer Organization and Design Fundamentals
2-bits – 4 levels 3-bits – 8 levels
4-bits – 16 levels 5-bits – 32 levels
Figure 2-8 Effects of Number of Bits on Roundoff Error
Aliasing is also the reason fluorescent lights are never used in
sawmills. Fluorescent lights blink much like a very fast strobe light and
can make objects appear as if they are not moving. If the frequency of
the fluorescent lights and the speed of a moving saw blade are
multiples of each other, it can appear as if the spinning blade is not
moving at all.
Both of these examples are situations where aliasing has occurred. If
a signal’s frequency is faster than the sampling rate, then information
will be lost, and the collected data will never be able to duplicate the
original.
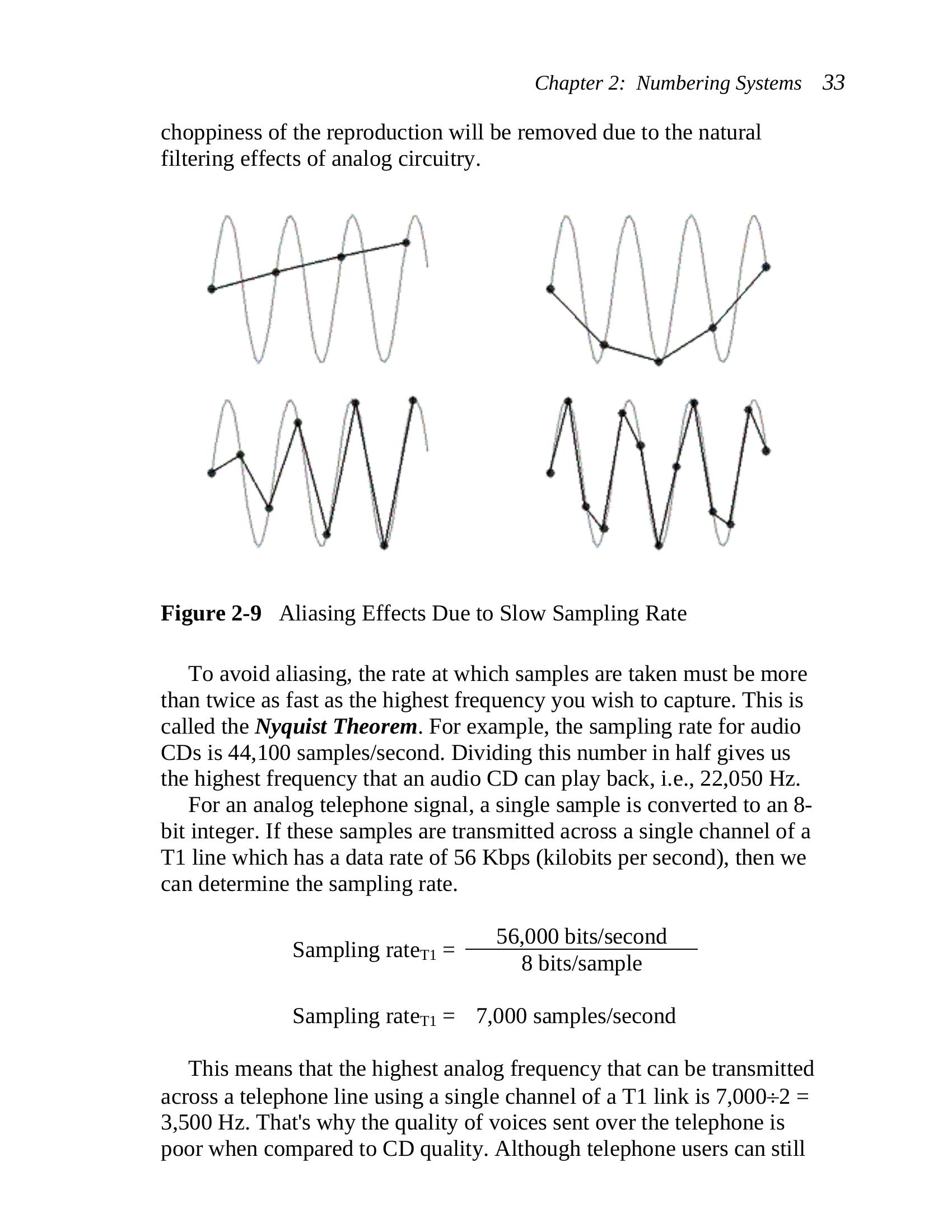
The graphs in Figure 2-9 show how different sampling rates can
result in different interpretations of the collected data, the dark points
representing the samples. Note that the bottom-right graph represents a
good sampling rate. When the computer reproduces the signal, the
| None | None | None | None | None | |
| None | None | None | |||
| None | None | None | None | None | |
| None | None | None | None | ||
| None | None | None | None | None | |
| None | None | None | |||
| None | None | None | None | None |
| None | |
| None | |
| None | |
| None | |
| None | |
| None |
Chapter 2: Numbering Systems 33
choppiness of the reproduction will be removed due to the natural
filtering effects of analog circuitry.
Figure 2-9 Aliasing Effects Due to Slow Sampling Rate
To avoid aliasing, the rate at which samples are taken must be more
than twice as fast as the highest frequency you wish to capture. This is
called the Nyquist Theorem. For example, the sampling rate for audio
CDs is 44,100 samples/second. Dividing this number in half gives us
the highest frequency that an audio CD can play back, i.e., 22,050 Hz.
For an analog telephone signal, a single sample is converted to an 8-
bit integer. If these samples are transmitted across a single channel of a
T1 line which has a data rate of 56 Kbps (kilobits per second), then we
can determine the sampling rate.
56,000 bits/second
Sampling rate =
T1
8 bits/sample
Sampling rate = 7,000 samples/second
T1
This means that the highest analog frequency that can be transmitted
across a telephone line using a single channel of a T1 link is 7,000÷2 =
3,500 Hz. That’s why the quality of voices sent over the telephone is
poor when compared to CD quality. Although telephone users can still
34 Computer Organization and Design Fundamentals
recognize the voice of the caller on the opposite end of the line when
the higher frequencies are eliminated, their speech often sounds muted.
2.7 Hexadecimal Representation
It is usually difficult for a person to look at a binary number and
instantly recognize its magnitude. Unless you are quite experienced at
using binary numbers, recognizing the relative magnitudes of
10101101 and 10100101 is not immediate (173 is greater than
2 2 10
165 ). Nor is it immediately apparent to us that 1001101101 equals
10 2
621 without going through the process of calculating 512 + 64 + 32 +
10
8 + 4 + 1.
There is another problem: we are prone to creating errors when
writing or typing binary numbers. As a quick exercise, write the binary
number 1001011111101101001000111 onto a sheet of paper. Did you
2
make a mistake? Most people would have made at least one error.
To make the binary representation of numbers easier on us humans,
there is a shorthand representation for binary values. It begins by
partitioning a binary number into its nibbles starting at the least
significant bit (LSB). An example is shown below:
The number: 1001011110110100100111
…can be divided into: 10 0101 1110 1101 0010 0111
Next, a symbol is used to represent each of the possible
combinations of bits in a nibble. We start by numbering them with the
decimal values equivalent to their binary value, i.e.:
0000 = 0
2 10
0001 = 1
2 10
0010 = 2
2 10
: : :
1000 = 8
2 10
1001 = 9
2 10
At 9, however, we run out of decimal characters. There are six more
nibbles to label, so we begin using letters: A, B, C, D, E, and F. These
represent the decimal values 10 , 11 , 12 , 13 , 14 , and 15
10 10 10 10 10 10
respectively.
| The number: | 1001011110110100100111 | None | None | None | None | None |
| …can be divided into: | 10 | 0101 | 1110 | 1101 | 0010 | 0111 |

Chapter 2: Numbering Systems 35
1010 = A
2
1011 = B
2
: : :
1111 = F
2
Table 2-1 presents the mapping between the sixteen patterns of 1’s
and 0’s in a binary nibble and their corresponding decimal and
hexadecimal (hex) values.
Table 2-1 Converting Binary to Decimal and Hexadecimal
Binary Decimal Hex Binary Decimal Hex
0000 0 0 1000 8 8
0001 1 1 1001 9 9
0010 2 2 1010 10 A
0011 3 3 1011 11 B
0100 4 4 1100 12 C
0101 5 5 1101 13 D
0110 6 6 1110 14 E
0111 7 7 1111 15 F
Another way to look at it is that hexadecimal counting is also similar
to decimal except that instead of having 10 numerals, it has sixteen.
This is also referred to as a base-16 numbering system.
How do we convert binary to hexadecimal? Begin by dividing the
binary number into its nibbles (if the number of bits is not divisible by
4, add leading zeros), then nibble-by-nibble use the table above to find
the hexadecimal equivalent to each 4-bit pattern. For example:
The number: 1001011110110100100111
…is divided into: 0010 0101 1110 1101 0010 0111
…which translates to: 2 5 E D 2 7
Therefore, 1001011110110100100111 = 25ED27 . Notice the use
2 16
of the subscript “16” to denote hexadecimal representation.
Going the other way is just as easy. Translating 5D3F21 to binary
16
goes something like this:
| Binary | Decimal | Hex | ||||||
| 0000 | None | None | 0 | None | None | 0 | None | None |
| 0001 | None | None | 1 | None | None | 1 | None | None |
| 0010 | None | None | 2 | None | None | 2 | None | None |
| 0011 | None | None | 3 | None | None | 3 | None | None |
| 0100 | None | None | 4 | None | None | 4 | None | None |
| 0101 | None | None | 5 | None | None | 5 | None | None |
| 0110 | None | None | 6 | None | None | 6 | None | None |
| 0111 | None | None | 7 | None | None | 7 | None | None |
| Binary | Decimal | Hex | ||||||
| 1000 | None | None | 8 | None | None | 8 | None | None |
| 1001 | None | None | 9 | None | None | 9 | None | None |
| 1010 | None | None | 10 | None | None | A | None | None |
| 1011 | None | None | 11 | None | None | B | None | None |
| 1100 | None | None | 12 | None | None | C | None | None |
| 1101 | None | None | 13 | None | None | D | None | None |
| 1110 | None | None | 14 | None | None | E | None | None |
| 1111 | None | None | 15 | None | None | F | None | None |
| The number: | 1001011110110100100111 | None | None | None | None | None |
| …is divided into: | 0010 | 0101 | 1110 | 1101 | 0010 | 0111 |
| …which translates to: | 2 | 5 | E | D | 2 | 7 |

36 Computer Organization and Design Fundamentals
The hexadecimal value: 5 D 3 F 2 1
…translates to: 0101 1101 0011 1111 0010 0001
Therefore, 5D3F21 = 010111010011111100100001 .
16 2
It is vital to note that computers do not use hexadecimal, humans do.
Hexadecimal provides humans with a reliable, short-hand method of
writing large binary numbers.
2.8 Binary Coded Decimal
When was the last time you multiplied your house number by 5? Or
have you ever added 215 to your social security number? These
questions seem silly, but they reveal an important fact about numbers.
Some numbers do not need to have mathematical operations performed
on them, and therefore, do not need to have a mathematically correct
representation in binary.
In an effort to afford decimal notation the same convenience of
conversion to binary that hex has, Binary Coded Decimal (BCD) was
developed. It allows for fast conversion to binary of integers that do not
require mathematical operations.
As in hex, each decimal digit represents a nibble of the binary
equivalent. Table 2-2 shows the conversion between each decimal digit
and the binary equivalent.
Table 2-2 Converting BCD to Decimal
BCD Decimal BCD Decimal
Nibble Digit Nibble Digit
0000 0 1000 8
0001 1 1001 9
0010 2 1010 Invalid
0011 3 1011 Invalid
0100 4 1100 Invalid
0101 5 1101 Invalid
0110 6 1110 Invalid
0111 7 1111 Invalid
For example, the BCD value 0001 0110 1001 0010 equals 1692 .
10
| The hexadecimal value: | 5 | D | 3 | F | 2 | 1 |
| …translates to: | 0101 | 1101 | 0011 | 1111 | 0010 | 0001 |
| BCD | Decimal | ||||
| None | Nibble | None | None | Digit | None |
| 0000 | None | None | 0 | None | None |
| 0001 | None | None | 1 | None | None |
| 0010 | None | None | 2 | None | None |
| 0011 | None | None | 3 | None | None |
| 0100 | None | None | 4 | None | None |
| 0101 | None | None | 5 | None | None |
| 0110 | None | None | 6 | None | None |
| 0111 | None | None | 7 | None | None |
| BCD | Decimal | ||||
| None | Nibble | None | None | Digit | None |
| 1000 | None | None | 8 | None | None |
| 1001 | None | None | 9 | None | None |
| 1010 | None | None | Invalid | None | None |
| 1011 | None | None | Invalid | None | None |
| 1100 | None | None | Invalid | None | None |
| 1101 | None | None | Invalid | None | None |
| 1110 | None | None | Invalid | None | None |
| 1111 | None | None | Invalid | None | None |

Chapter 2: Numbering Systems 37
It is important to note that there is no algorithmic conversion
between BCD and decimal. BCD is only a method for representing
decimal numbers in binary.
Another item of note is that not all binary numbers convert from
BCD to decimal. 0101 1011 0101 for example is an illegal BCD value
because the second nibble, 1011, does not have a corresponding
decimal value.
There are two primary advantages of BCD over binary. First, any
mathematical operation based on a factor of ten is simpler in BCD.
Multiplication by ten, for example, appends a nibble of zeros to the
right side of the number. All it takes to truncate or round a base-10
value in BCD is to zero the appropriate nibbles. Because of this
advantage, BCD is used frequently in financial applications due to legal
requirements that decimal values be exactly represented. Binary cannot
do this for fractions as we shall see in Chapter 3.
The second advantage is that conversion between entered or
displayed numeric characters and the binary value being stored is fast
and does not require much code.
The primary disadvantage is that unless the operation is based on a
power of ten, mathematical operations are more complex and require
more hardware. In addition, BCD is not as compact as unsigned binary
and may require more memory for storage.
BCD can be used to represent signed values too, although there are
many implementations. Different processor manufacturers use different
methods making it hard to select a standard. One of the easiest ways to
represent negative numbers in BCD is to add a nibble at the beginning
of the number to act as a plus/minus sign. By using one of the illegal
BCD values to represent a negative sign and another to represent a
positive sign, BCD values can be made negative or positive. Binary
values of 1010, 1100, or 1110 typically mean the number is positive
while binary values of 1011 or 1101 mean the number is negative. For
example, –1234 in signed BCD would be 1101 0001 0010 0011 0100
while +1234 would be 1100 0001 0010 0011 0100. BCD values
preceded with 1111 typically indicate unsigned values.
2.9 Gray Codes
The use of binary counting sequences is common in digital
applications. For example, an n-bit binary value can be used to identify
the position of a rotating shaft as being within one of 2n different arcs.

38 Computer Organization and Design Fundamentals
As the shaft turns, a sensor can detect which of the shaft’s arcs it is
aligned with by reading a digital value and associating it with a specific
arc. By remembering the previous position and timing the changes
between positions, a processor can also compute speed and direction.
Figure 2-10 shows how a shaft’s position might be divided into eight
arcs using three bits. This would allow a processor to determine the
shaft’s position to within 360o/8 = 45o.
000
001
111
010
110
011
101
100
Figure 2-10 Eight Binary Values Identifying Rotating Shaft Position
One type of shaft position sensor uses a disk mounted to the shaft
with slots cut into the disk at different radii representing different bits.
Light sources are placed on one side of the disk while sensors on the
other side of the disk detect when a hole is present, i.e., the sensor is
receiving light. Figure 2-11 presents a disk that might be used to
identify the shaft positions of the example from Figure 2-10.
Sensor
Light Sources
Figure 2-11 Example of a Position Encoder

Chapter 2: Numbering Systems 39
In its current position in the figure, the slots in the disk are lined up
between the second and third light sensors, but not the first. This means
that the sensor will read a value of 110 indicating the shaft is in
position number 110 = 6.
2
There is a potential problem with this method of encoding. It is
possible to read the sensor at the instant when more than one gap is
opening or closing between its light source and sensor. When this
happens, some of the bit changes may be detected while others are not.
If this happens, an erroneous measurement may occur.
For example, if the shaft shown above turns clockwise toward
position 101 = 5, but at the instant when the sensor is read, only the
2
first bit change is detected, then the value read will be 111 = 7
2
indicating counter-clockwise rotation.
To solve this problem, alternate counting sequences referred to as
the Gray code are used. These sequences have only one bit change
between values. For example, the values assigned to the arcs of the
above shaft could follow the sequence 000, 001, 011, 010, 110, 111,
101, 100. This sequence is not correct numerically, but as the shaft
turns, only one bit will change as the shaft turns from one position to
the next.
There is an algorithm to convert an n-bit unsigned binary value to its
corresponding n-bit Gray code. Begin by adding a 0 to the most
significant end of the unsigned binary value. There should now be n
boundaries between the n+1 bits. For each boundary, write a 0 if the
adjacent bits are the same and a 1 if the adjacent bits are different. The
resulting value is the corresponding n-bit Gray code value. Figure 2-12
presents an example converting the 6 bit value 100011 to Gray code.
2
Add zero to left-
0 1 0 0 0 1 1
most side of the
value to convert
1 1 0 0 1 0
Adjacent bits that are Adjacent bits that are
different generate a 1. the same generate a 0.
Figure 2-12 Conversion from Unsigned Binary to Gray Code
| 1 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 0 |

40 Computer Organization and Design Fundamentals
Using this method, the Gray code for any binary value can be
determined. Table 2-3 presents the full Gray code sequence for four
bits. The shaded bits in third column are bits that are different then the
bit immediately to their left. These are the bits that will become ones in
the Gray code sequence while the bits not shaded are the ones that will
be zeros. Notice that exactly one bit changes in the Gray code from one
row to the next and from the bottom row to the top row.
Table 2-3 Derivation of the Four-Bit Gray Code
Binary
Gray
Decimal Binary w/starting
Code
zero
0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 0 0 0 1 0 0 0 0 1 0 0 0 1
2 0 0 1 0 0 0 0 1 0 0 0 1 1
3 0 0 1 1 0 0 0 1 1 0 0 1 0
4 0 1 0 0 0 0 1 0 0 0 1 1 0
5 0 1 0 1 0 0 1 0 1 0 1 1 1
6 0 1 1 0 0 0 1 1 0 0 1 0 1
7 0 1 1 1 0 0 1 1 1 0 1 0 0
8 1 0 0 0 0 1 0 0 0 1 1 0 0
9 1 0 0 1 0 1 0 0 1 1 1 0 1
10 1 0 1 0 0 1 0 1 0 1 1 1 1
11 1 0 1 1 0 1 0 1 1 1 1 1 0
12 1 1 0 0 0 1 1 0 0 1 0 1 0
13 1 1 0 1 0 1 1 0 1 1 0 1 1
14 1 1 1 0 0 1 1 1 0 1 0 0 1
15 1 1 1 1 0 1 1 1 1 1 0 0 0
2.10 What’s Next?
In this chapter, we’ve covered the different methods of representing
values, specifically positive integers, using digital circuitry. In addition
to counting integers, the issues surrounding the conversion of analog or
“real world” values to digital were examined along with some of the
problems encountered when sampling. Finally, two methods of binary
representation were presented: hexadecimal and BCD.
| Decimal | Binary | Binary | None | None | None | None | None | None | None | None | Gray Code |
None | None | None | None | None | None | None | None | ||
| None | None | None | w/starting | None | None | None | None | None | None | None | None | None | None | None | None | None | None | None | None | None | None |
| None | None | None | zero | None | None | None | None | None | None | None | None | None | None | None | None | None | None | None | None | None | None |
| 0 | 0 0 0 0 | 0 0 0 0 0 | None | None | None | None | None | None | None | None | None | None | 0 0 0 0 | None | None | None | None | None | None | None | None |
| 1 | 0 0 0 1 | 0 0 0 0 | None | None | None | None | None | None | None | 1 | None | 0 0 0 | None | None | None | None | None | None | 1 | ||
| 2 | 0 0 1 0 | 0 0 0 | None | None | None | None | None | 1 0 | None | None | None | 0 0 | None | None | None | None | 1 1 | None | None | ||
| 3 | 0 0 1 1 | 0 0 0 | None | None | None | None | None | 1 | 1 | None | None | None | 0 0 | None | None | None | None | 1 | 0 | None | None |
| 4 | 0 1 0 0 | 0 0 | None | None | None | 1 0 | None | None | 0 | None | None | None | 0 | None | None | 1 1 | None | None | 0 | None | None |
| 5 | 0 1 0 1 | 0 0 | None | None | None | 1 0 1 | None | None | None | None | None | 0 | None | None | 1 1 1 | None | None | None | None | ||
| 6 | 0 1 1 0 | 0 0 | None | None | None | 1 | 1 | None | None | 0 | None | 0 | None | None | 1 | 0 | None | None | 1 | ||
| 7 | 0 1 1 1 | 0 0 | None | None | None | 1 | 1 1 | None | None | None | None | None | 0 | None | None | 1 | 0 0 | None | None | None | None |
| 8 | 1 0 0 0 | 0 | None | 1 0 | None | None | 0 0 | None | None | None | None | None | 1 1 | None | None | 0 0 | None | None | None | None | |
| 9 | 1 0 0 1 | 0 | None | 1 0 | None | None | 0 | None | None | 1 | None | 1 1 | None | None | 0 | None | None | 1 | |||
| 10 | 1 0 1 0 | 0 | None | 1 0 1 0 | None | None | None | None | None | None | None | 1 1 1 1 | None | None | None | None | None | None | |||
| 11 | 1 0 1 1 | 0 | None | 1 0 1 | None | None | None | None | 1 | None | None | None | 1 1 1 | None | None | None | None | 0 | None | None | |
| 12 | 1 1 0 0 | 0 | None | 1 | 1 | None | None | 0 | 0 | None | None | None | 1 | 0 | None | None | 1 | 0 | None | None | |
| 13 | 1 1 0 1 | 0 | None | 1 | 1 | None | None | 0 1 | None | None | None | 1 | 0 | None | None | 1 1 | None | None | |||
| 14 | 1 1 1 0 | 0 | None | 1 | 1 1 | None | None | None | None | 0 | None | 1 | 0 0 | None | None | None | None | 1 | |||
| 15 | 1 1 1 1 | 0 | None | 1 | 1 1 1 | None | None | None | None | None | None | None | 1 | 0 0 0 | None | None | None | None | None | None |
| Gray |
| Code |

Chapter 2: Numbering Systems 41
Chapter 3 examines the special needs surrounding the digital
representation of addition, subtraction, and floating-point values. It also
introduces the operation of the processor in handling some arithmetic
functions.
Problems
1. What is the minimum number of bits needed to represent 768
10
using unsigned binary representation?
2. What is the largest possible integer that can be represented with a
6-bit unsigned binary number?
3. Convert each of the following values to decimal.
a) 10011101 b) 10101 c) 111001101 d) 01101001
2 2 2 2
4. Convert each of the following values to an 8-bit unsigned binary
value.
a) 35 b) 100 c) 222 d) 145
10 10 10 10
5. If an 8-bit binary number is used to represent an analog value in
the range from 0 to 100 , what does the binary value 01100100
10 10 2
represent?
6. If an 8-bit binary number is used to represent an analog value in
the range from 32 to 212, what is the accuracy of the system? In
other words, if the binary number is incremented by one, how
much change does it represent in the analog value?
7. Assume a digital to analog conversion system uses a 10-bit integer
to represent an analog temperature over a range of -25oF to 125oF.
If the actual temperature being read was 65.325oF, what would be
the closest possible value that the system could represent?
8. What is the minimum sampling rate needed in order to successfully
capture frequencies up to 155 KHz in an analog signal?
9. Convert the following numbers to hexadecimal.
a) 1010111100101100011
2
b) 10010101001001101001
2
c) 01101101001010011001
2
d) 10101100100010
2
10. Convert each of the following hexadecimal values to binary.
a) ABCD b) 1DEF c) 8645 d) 925A
16 16 16 16

42 Computer Organization and Design Fundamentals
11. True or False: A list of numbers to be added would be a good
candidate for conversion using BCD.
12. Determine which of the following binary patterns represent valid
BCD numbers (signed or unsigned). Convert the valid ones to
decimal.
a.) 1010111100101100011
b.) 10010101001001101001
c.) 01101101001010011001
d.) 11000110010000010000
e.) 1101100101110010
f.) 111100010010010101101000
g.) 10101100100010
13. Convert the decimal number 96404 to BCD.
10
14. Create the 5-bit Gray code sequence.